場路結合時空調制CST仿真實例
這期我們的案例是Spatiotemporal modulation, 時空調制。這種效果能夠打破互易性,用來設計微波或光子通信中的非互易設備。
Step1. 基本結構
基于兩個金屬換的簡單諧振超表面,Floquet 仿真可得兩種圓極化的諧振頻率一致:


Step 2. 添加端口
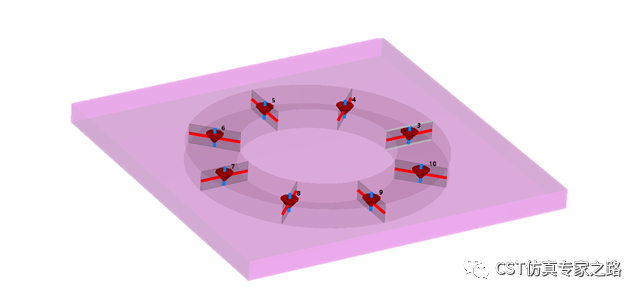
這里是要添加8個變容二極管,用0.1GHz的電壓控制電容值,每個電容之間有相位差,所以在時間和空間上對結構電容性進行調節,達到改變諧振頻率的目的。
Step 3. 電路
變容二極管的查看電容變化方法我們已經在“如何獲取壓變電容(變容二極管)的電容曲線”一文中寫了。
這里多設計兩個濾波電路,增加二極管和三維結構直接的隔離。這里可用S參數任務查看加上這些被動元件后的S11,可見諧振為8.6GHz,和沒有電路時的8.9GHz差不多。

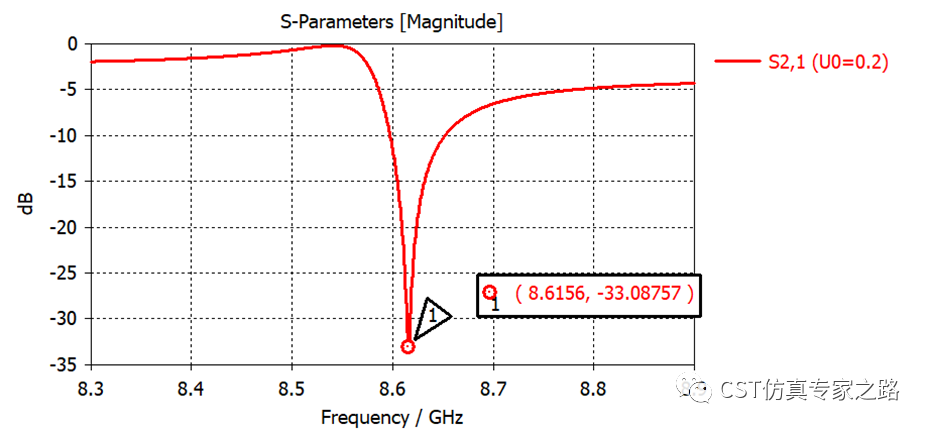
注意這里用的還是恒定電壓,還沒有加時變電壓調制。
Step 4. 調制的S參數
“如何在電路中獲得S參數 - 9個方法”一文中介紹過幾個電路中獲得S參數的方法,這里正好排上用場。
可用頻譜線任務或瞬態任務,細節就跳過了,直接上兩個方法用的電路和關鍵結果。
頻譜任務:
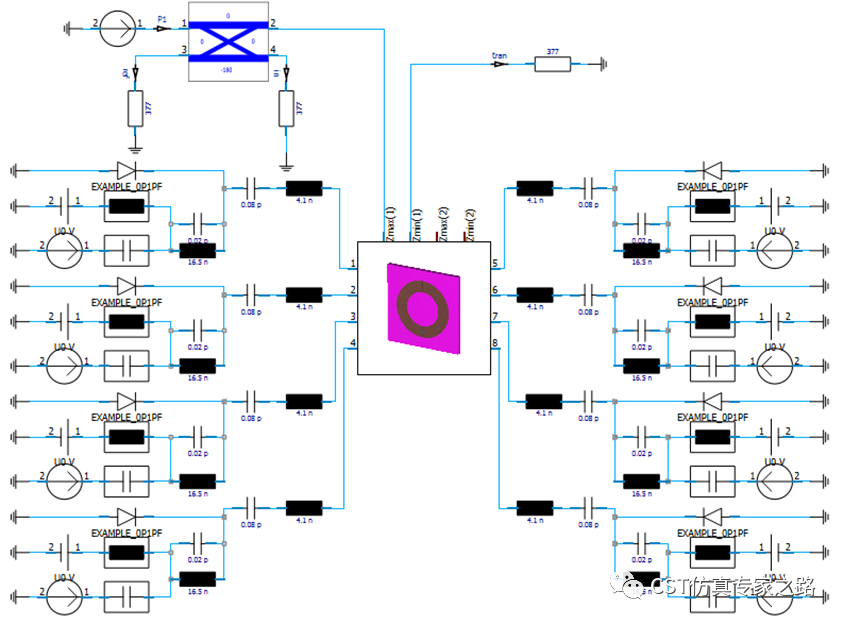

瞬態任務:


對比兩個方法S11,結果一致,可見已經將0.1GHz調制進8.6GHz的諧振中:

小結:
1. 本案例是個非常高級巧妙的場路結合案例。
2. 時空調制電路可用CST電路中計算, 變容二極管也可以用CST的電路查看性能。
3. 很多粉絲后臺問各種案例怎么做,復雜案例其實都是簡單的操作組合起來的哦!
參考文獻:Sounas, D. L., Caloz, C., & Alù, A. (2013).Giant non-reciprocity at the subwavelength scale using angular momentum-biasedmetamaterials. Nature Communications, 4(1). doi:10.1038/ncomms3407





