CST分析表面等離子極化激元SPP實例(5)- 一維光柵耦合,衍射模式,Floquet端口
下面兩期我們看一下衍射光柵的高階衍射、衍射效率、反射率。具體到仿真設置,就是Floquet端口的模式分析,S參數與衍射效率和反射率的關系。那么研究這些衍射和表面等離子極化激元SPP有什么關系呢?關系可大了,光柵是一種能夠用來激勵出SPP模式的結構,所以我們要了解其衍射特性,才能激勵出表面波SPP。
使用等離子激元單元模板,開啟計算透射率反射率吸收率:

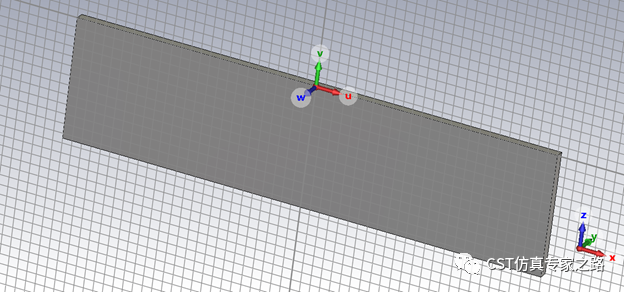
添加銀材料,畫個因材料的基底,這里d是光柵周期長度,1000納米:

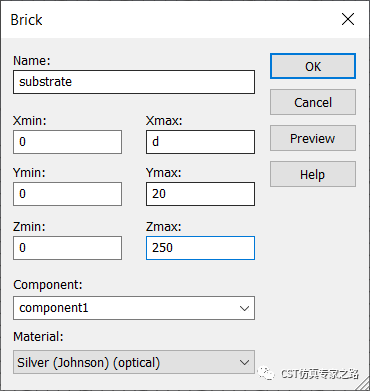
將WCS移至上方中間,添加光柵,這里ratio是光柵與周期的比,可放0.5,h是光柵高度,可放250:
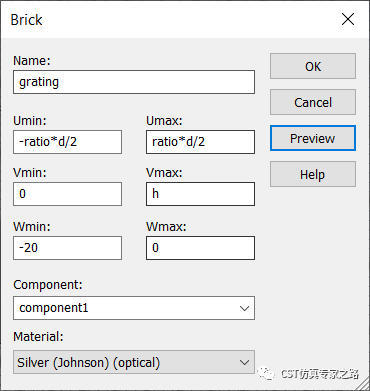
Z+方向加1000:
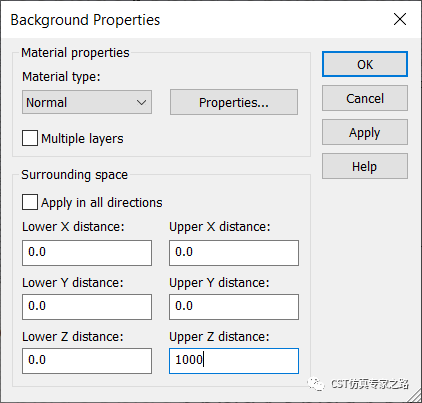
Z-方形電邊界,其他為Unit Cell:
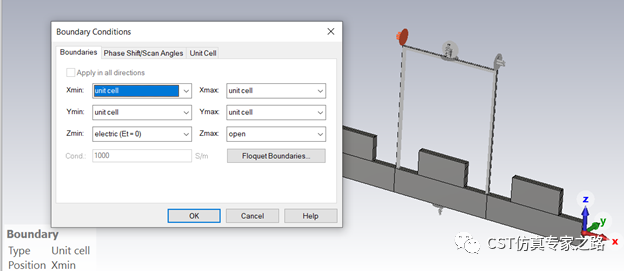
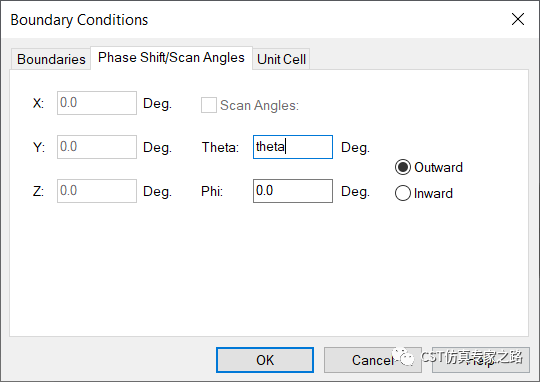
邊界掃描角設theta,初始為0(垂直入射):
進入Zmax端口:
可見該尺寸有6個模可傳播(有beta值),這樣我們將仿真模數改成6:
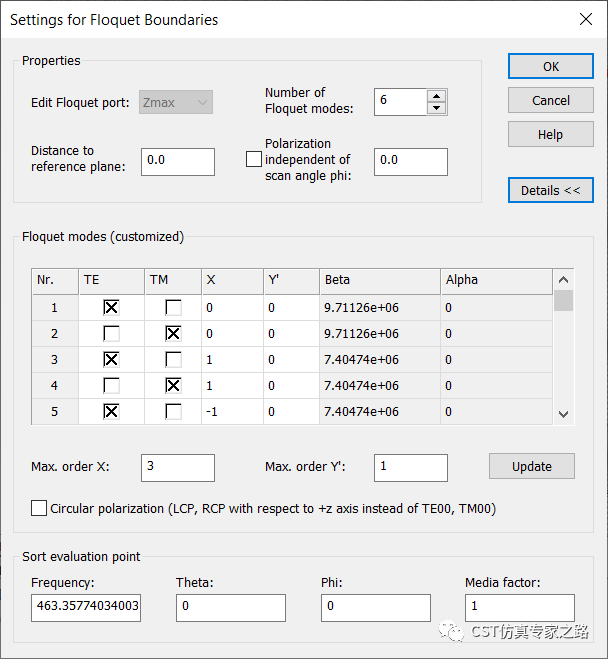
注意這里截圖只顯示了前5個模式。6個模式分別是:
TE(0,0),TM(0,0),TE(1,0),TM (1,0),TE(-1,0),TM (-1,0)。
括號里第一個數字對應X,對應光柵衍射中的0階,1階和-1階模式;第二個數值對應Y‘,都是0就是指1維光柵。
如果下拉列表就可以看到可傳播的模式有beta傳播常數,不可傳播的模式則是alpha衰減系數。
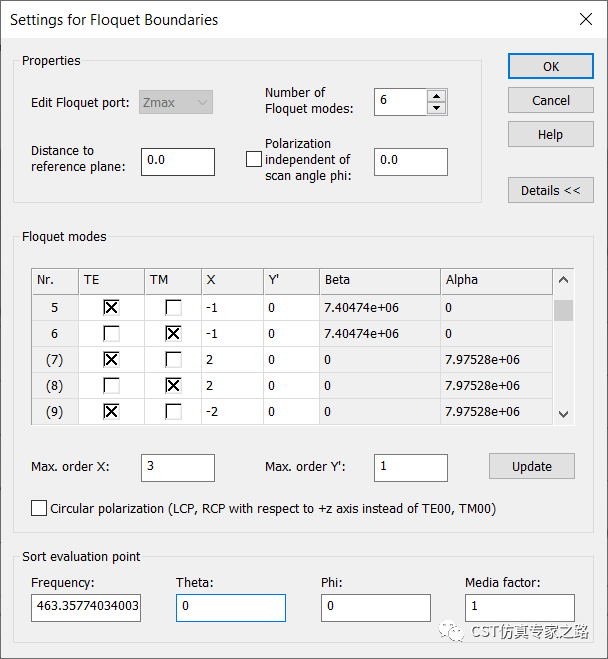
還要注意,這下面的Theta是0,表示這些模式beta和alpha分析的是垂直入射的情況;如果將Theta改成45度,點擊update,模式就都更新了,雖然還是只有6個傳播模,但是X發生改變,階數不同了。
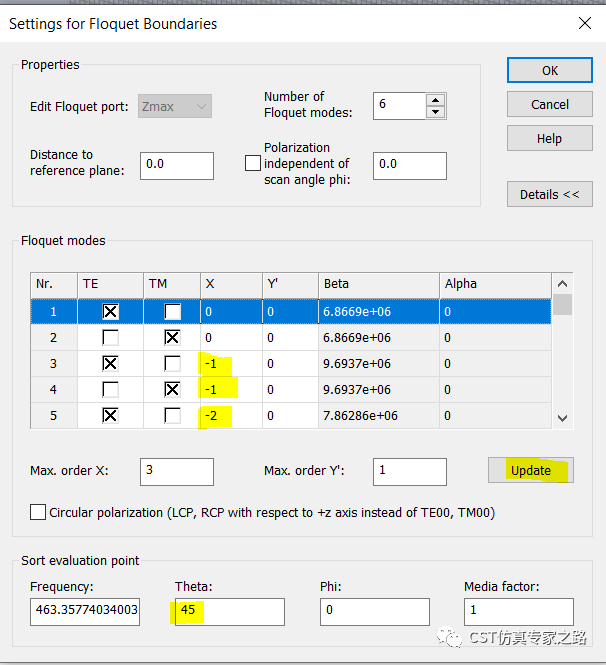
所以,在我們等一下研究入射角時,我們就要增加計算模式,比如10個模式,這樣就包括了-2階,-1階,0階,1階和2階。更要注意,這個theta和邊界掃描角參數theta作用不同,這里只是計算模式參數,邊界那個是真正用來掃描入射角的。
1. 垂直入射的衍射模:
Theta先用0,我們在求解器中,選擇Zmax端口只激勵兩個基礎模,因為我們要仿真出光柵的衍射,而不是用衍射作為輸入仿真。這里選擇一個自動的頻點進行仿真,也就是求解器的頻點。
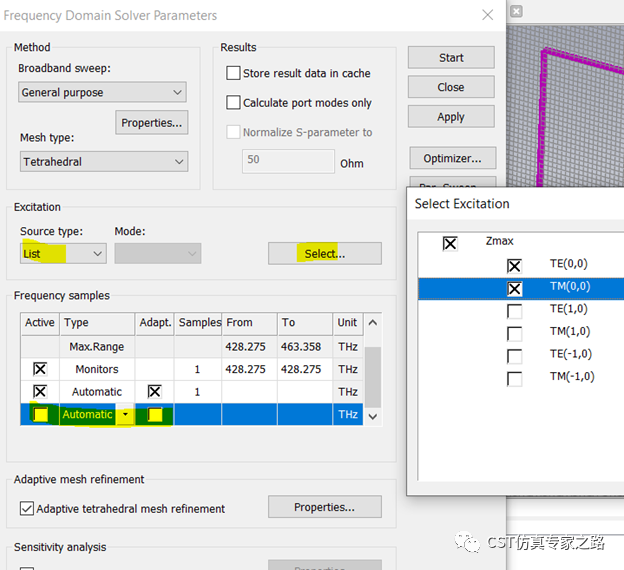
仿真結束,看S參數,先看TE模,S11反射不高,主要以S31和S51兩個模式傳出能量,其他S21,S41和S61可忽略,因為他們是TE與TM模轉換,這里基本不涉及。同理TM模S參數效果相同。
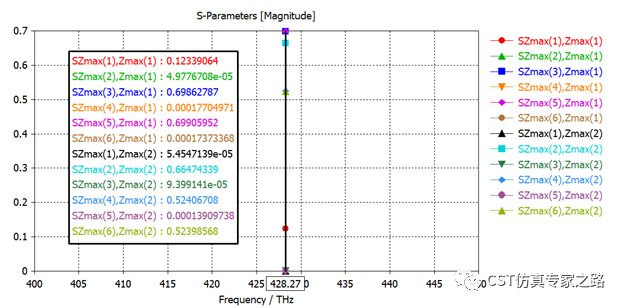
查看模式場,垂直入射的TE(0,0)模:
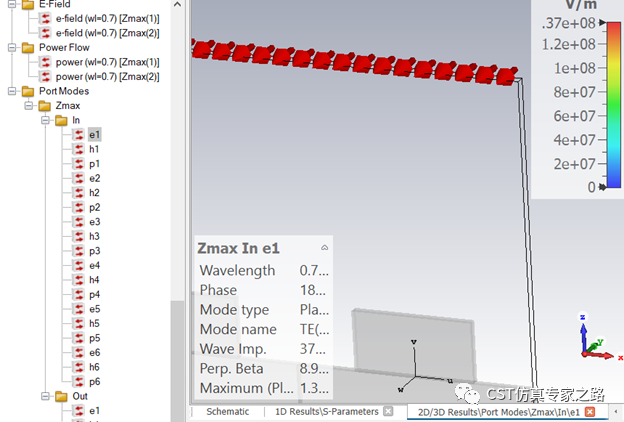
該模激勵出來的電場:

垂直入射的TM(0,0)模:
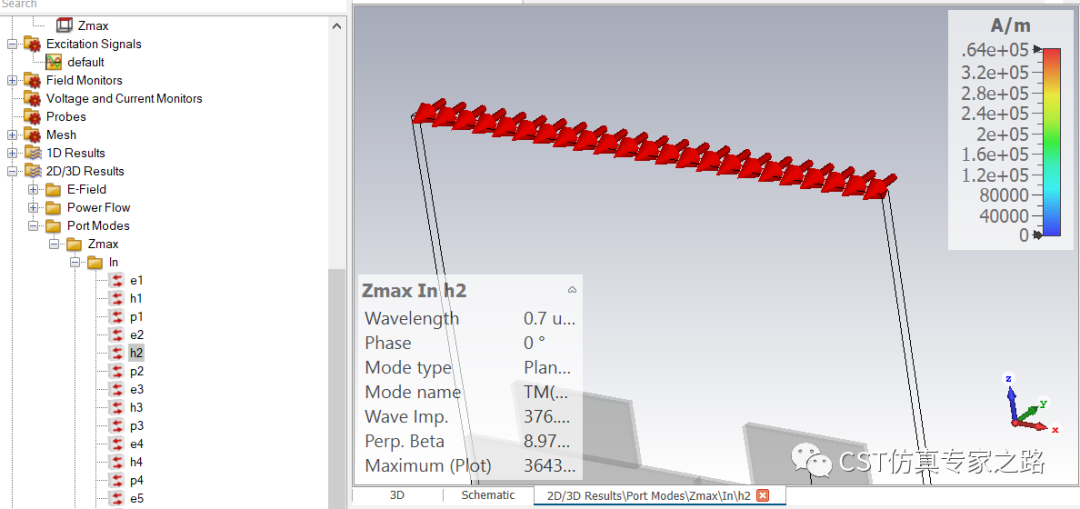
該模激勵出來的電場:

垂直反射回來的0階衍射模TE(0,0)和TM(0,0)就不顯示了,很好理解,下面看看高階模方向。
反射的1階衍射模TE(1,0)方向:

反射的1階衍射模TM(1,0)方向:

反射的-1階衍射模TE(1,0)方向:
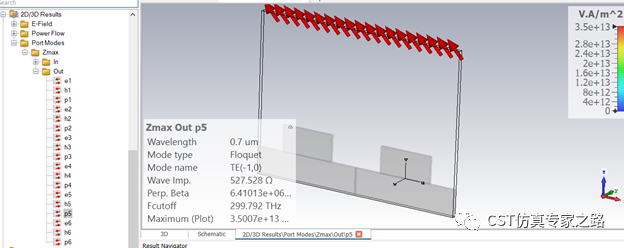
反射的-1階衍射模TM(1,0)方向:
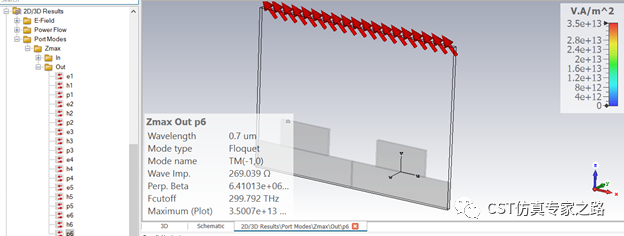
可見這種方形的光柵差不多把垂直入射波衍射到了兩邊45度角左右,能量比垂直反射回去要高很多,這就是光柵的模式調節作用。
對于垂直入射的模式,就是對應公式中的m:
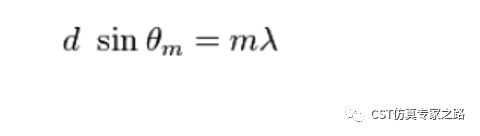
2. 凹槽深度(groove depth)與衍射效率
該光柵早在1982年就被分析過了,文獻中給出了1階衍射效率和吸收率,分別與光柵深度的關系(TE):
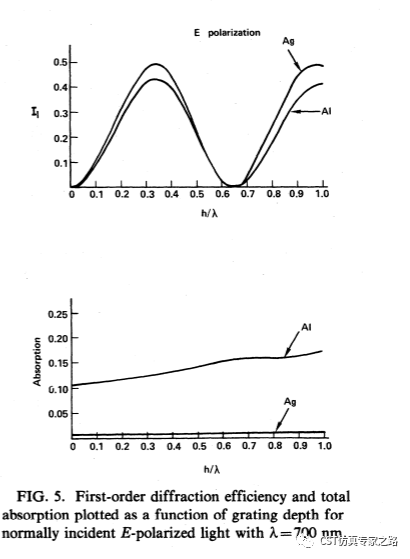
這就需要用到模板幫我們添加好的這些結果了:

R是反射率,T是透射率,A是吸收率。在這里的透射率是指不同模式之間的轉換能量,也就是光柵模式衍射的效率。那么這個E極化的1階衍射效率是哪個T結果呢?是T31。文獻還給了H極化的1階衍射效率和吸收率,這個是T42。
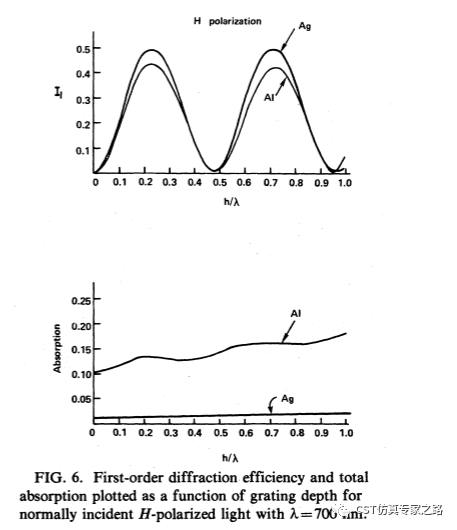
所以,我們所需要做的就是掃描參數h了:
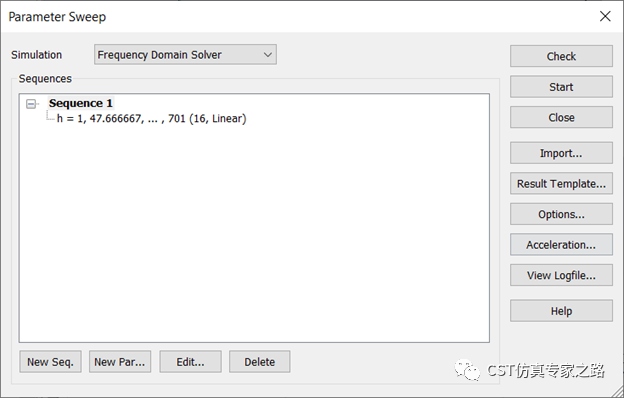
掃描結束后,可用后處理將離散1D結果合并成0D曲線:

四個結果,四個處理,我就不改名了,



可見與文獻結果一致。
3. 掃描入射角
文件另存,將參數改成以下數據:
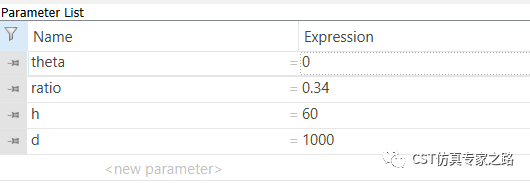
波長看647.1納米:

除了材料庫中的銀,我們自己添加Drude模型銀材料:
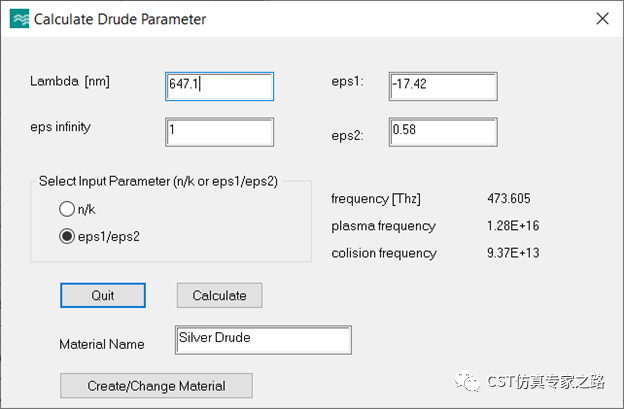
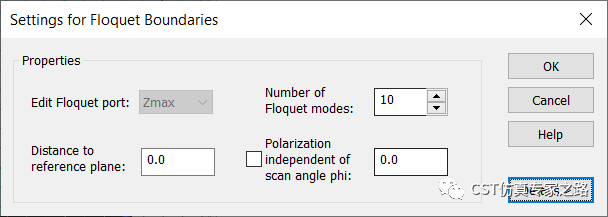
由于要掃描入射角,所以Floquet模式數量要增加,計算高階衍射:
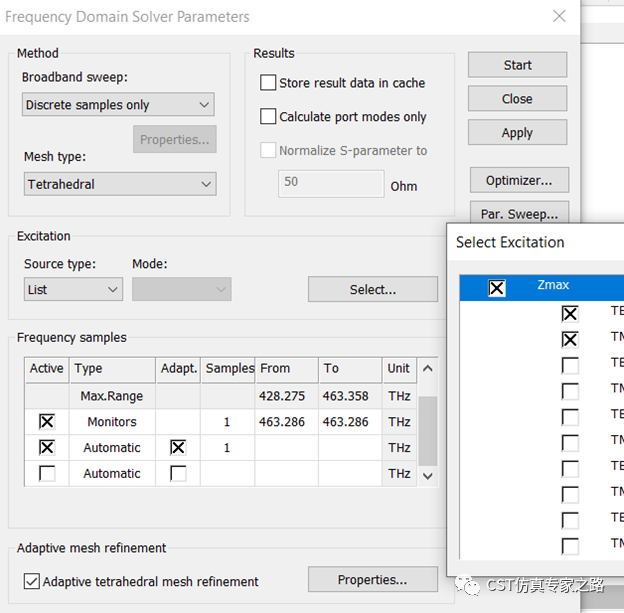
頻域求解器還是計算1個頻點,兩個基礎模:
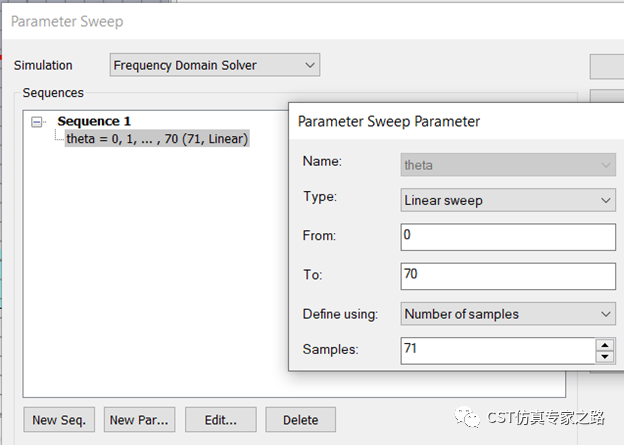
參數掃描Theta到70度,開始。
掃描過后,反射率會在結果文件夾中,不過都是一些離散頻點,需要換成0D曲線:
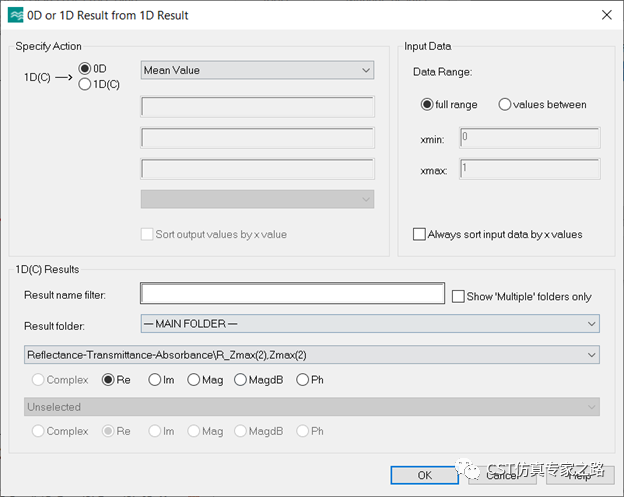
對兩個R11分別提取0D結果:
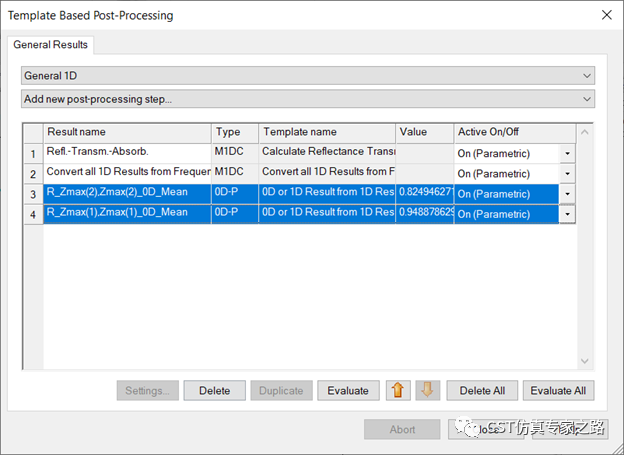
查看曲線,可見兩個基礎模的反射效果并不一樣:
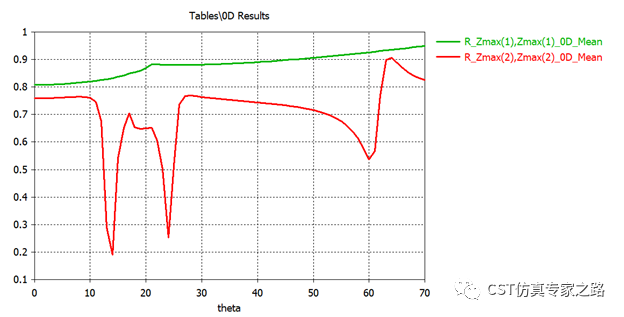
這個現象熟悉表面等離子激元的朋友肯定能猜到了,就是TM才能激勵出SPR模,TE不行,TE是很單調的(monotone behavior)。換句話說,在入射角為14,24和60度時,TM模發散能量很低,那能量去哪里了?答案是表面傳播了,只有TM模(也叫H極化、p極化或P-偏振光)可在該光柵表面激勵起等離子極化激元。
必須和文獻中計算和測量的一致:
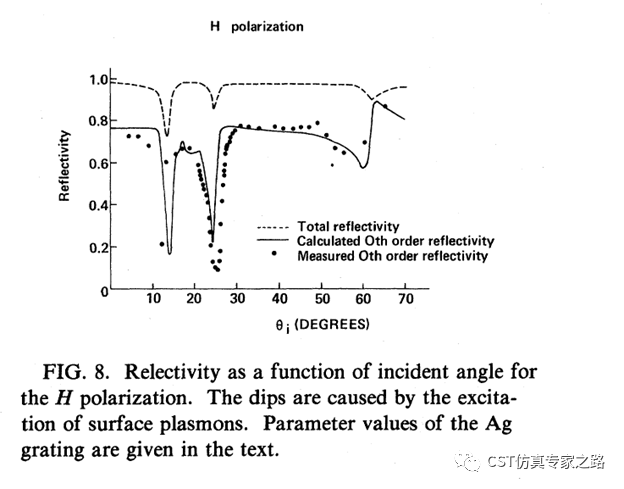
如果還不明白就看動圖:
theta=14度:

theta=24度:

theta=30度(非表面傳播):

參考:
Sheng, P., Stepleman, R. S., &Sanda, P. N. (1982). Exact eigenfunctions for square-wave gratings: Applicationto diffraction and surface-plasmon calculations. Physical Review B, 26(6),2907–2916. doi:10.1103/physrevb.26.2907
小結:
1. F-solver的Floquet端口模式對應光柵衍射的模式,方便我們研究光衍射,以及用光柵激勵SPP。
2. 如果材料庫中的光學材料色散與所需的不同,可用本案例提到的宏,生成drude模型材料。
3. (光)透射率(Transmittance)在光柵衍射分析時可以是衍射率(diffraction efficiency)哦!搞清楚Floquet模式就不會搞混定義了。





