使用CST微波工作室的時域求解器仿真電大問題的理論分析
首先給出兩個實際的仿真例子:
參考計算機:HP XW8400工作站,雙路雙核志強 5160 處理器,主頻 3.0GHz,內存16GB
基本數據:CST 微波工作室時域求解器每1000 萬個六面體網格占用1GB 內存;每1000 萬網格計算時間為 80 分鐘。電尺寸越大,上述統計數據越準確。
a) 108個波長賦形反射面天線,9.2米寬,4.75米高,2.9GHz 頻率。網格點數:8387 萬,計算時間:12小時 34分,占用內存:9.4GB。
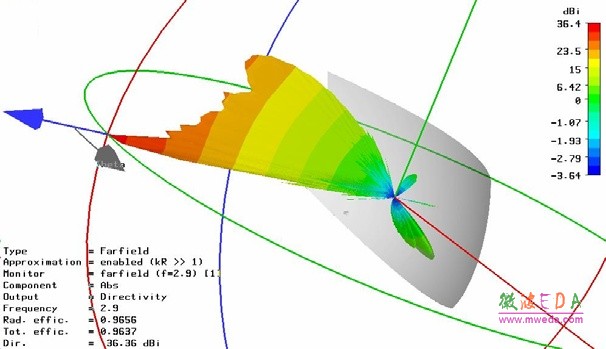
b) 圓錐對數螺旋天線分析,天線尺寸和仿真所得2GHz 時的方向圖如下所示。網格點數:666.4 萬,計算時間:1 小時5 分,占用內存:1.67GB。

1) 基本理論依據
由數學結論可知,頻域矩量法或邊界元法、頻域有限元法和時域有限積分法三者的計算量(體現在CPU 時間和所需內存)分別正比于所網格數N的3 次、2 次和1.1-1.2次方。當結構的電尺寸比較大或結構比較復雜時,網格點則逐漸增大,對于目前主流的32 位計算機(2GBytes 內存/2.6GHz 主頻/單 CPU)來說,前兩者將不再能夠勝任網格數達到幾萬和幾十萬的作業。而時域有限積分法則可處理800-1000 萬點(操作系統和顯卡要占500MB 的內 存),約8 小時CPU 時間一次完成幾個到數十個倍頻程的全部仿真。這個快速寬帶仿真特點歸功于時域有限積分法的顯式算法。
另一方面,三者的仿真速度是由各自算法所決定的。換言之,即便是采用64 位計算機,它們三者的速度的相對關系是不會改變的。有些人錯誤地認為,64 位機能夠提高速度,其實是64 位機由于它們的尋址空間大大地增加便可以“接受”大網格點的仿真問題了,不像32 位計算機有2-3GBytes 最大可接受文件的限制。可是,“接受”或能夠仿真絕不意味著它們的計算速度就提高了。其實,原來固有的3 次方、2 次方和1.1-1.2 次方的計算量依然不變,即所需的CPU時間同樣還是這么多。舉例來說,對于頻域有限元法,10 萬個網格點若需要10小時CPU,則100 萬個網格點需1000 小時!這個N 平方關系與32 位還是64 位計算機無關。內存需求同樣滿足N 的平方關系。故導致100 萬個網格點32 位機無法計算,但64 位機則可以,只要其物理內存足夠的大。這就是計算速度及內存需求與網格點關系的通用解釋。請注意:CPU 數目的增加一般是線性的(目前主流64 PC 工作站最大支持16 個CPUs)。況且,它還受到硬件投資的約束。
再看對計算機的要求。CST MWS 中的時域求解器由于采用時域有限積分算法,在數學上沒有矩陣求逆的過程,而有限元法是必須要做矩陣求逆,所以對計算機配置要求比較低。舉一個具體例子,一個內存 1GB 的普通計算機,CST MWS-T 可仿真800 萬個六面體網格的結構;而同樣配置下,頻域有限元軟件不超過20 萬個四面體網格。
2) CST MWS的專有技術
CST MWS專有的PBA 和TST技術,在保證精度的情況下,極大的降低了內存需求,提高計算速度。
1998年引入了專有的 PBA™(Perfect Boundary Approximation™)技術,使 CST MWS的結構逼近趨近完美。此方法采用精確共形網格插值的方式,彌補了經典 FDTD 算法對曲面物體采用階梯網格逼近的缺點,同時又保持了網格劃分容易、對大問題快速及內存需求小這三大原有的優點。
2002 年又引入了 TST™(Thin Sheet Technology™)薄片技術,在程序內部,通過對細線和薄片的專門處理,大大地提升了對這兩類問題的仿真度,使得軟件不但速度快,內存需求低,而且精度高。對于某些特殊問題,如共形天線,直接采用粗大網格,不用特殊的處理,就可精確仿真。
2004 年引入了 MSS™(Multilevel Subgridding Scheme™)多級子網技術,使網格使用更為經濟和有效,大大地減少了網格點,從而提升了仿真速度。
3) CST MWS中包含七個不同的算法或求解器
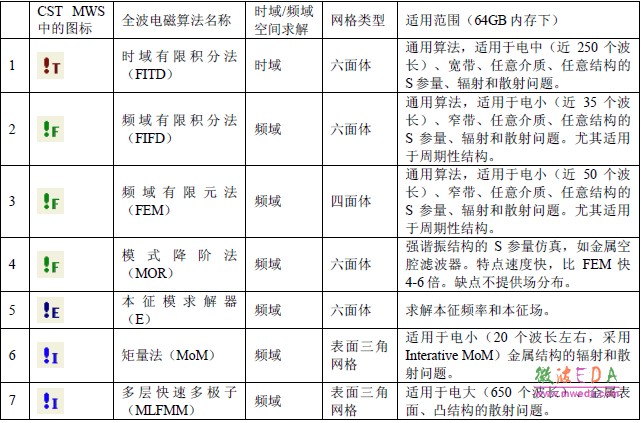
所有七種求解器全部集成于同一個界面,用戶可以根據不同問題自由選擇最合適的算法。盡管時域有限積分法的應用范圍最為寬廣,對于周期性結構,采用頻域有限元最為有效;對于高Q 值濾波器,采用MOR 最快;對于微調公差分析,六面體網格的算法有絕對的優勢;對于電大金屬凸結構的散射分析,最好采用 MLFMM 算法等等。
-

CST中文視頻教程,資深專家講解,視頻操作演示,從基礎講起,循序漸進,并結合最新工程案例,幫您快速學習掌握CST的設計應用...【詳細介紹】
推薦課程
-
7套中文視頻教程,2本教材,樣樣經典
-
國內最權威、經典的ADS培訓教程套裝
-
最全面的微波射頻仿真設計培訓合集
-
首套Ansoft Designer中文培訓教材
-
矢網,頻譜儀,信號源...,樣樣精通
-
與業界連接緊密的課程,學以致用...
-
業界大牛Les Besser的培訓課程...
-
Allegro,PADS,PCB設計,其實很簡單..
-
Hyperlynx,SIwave,助你解決SI問題
-
現場講授,實時交流,工作學習兩不誤






