超材料光子晶體CST仿真 - 60度周期布里淵區(qū)與布洛赫定理
之前寫過二維光子晶體的案例:超材料光子晶體和禁帶分析實(shí)例,其周期為正方形
這期我們還以二維光子晶體為例,看一下六邊形周期結(jié)構(gòu)的色散圖仿真,以及多重模式下利用布洛赫定理進(jìn)行模式挑選。
第一部分:建模和仿真設(shè)置
首先推薦使用色散圖模板,頻率范圍設(shè)0-250THz。


定義周期結(jié)構(gòu)尺寸參數(shù):

建模:
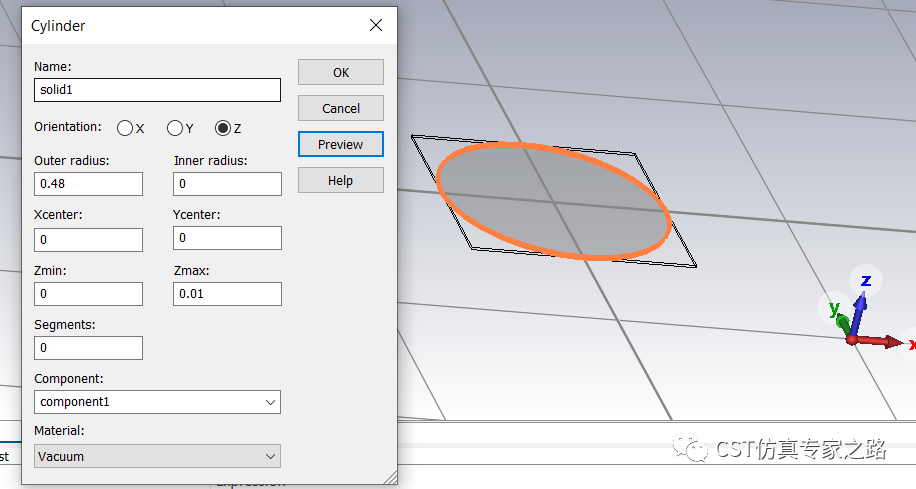
再畫個(gè)方型區(qū)域作為單元晶胞,用圓柱Trim。

復(fù)制周期單元,剪切,只保留方形區(qū)域內(nèi)單元:

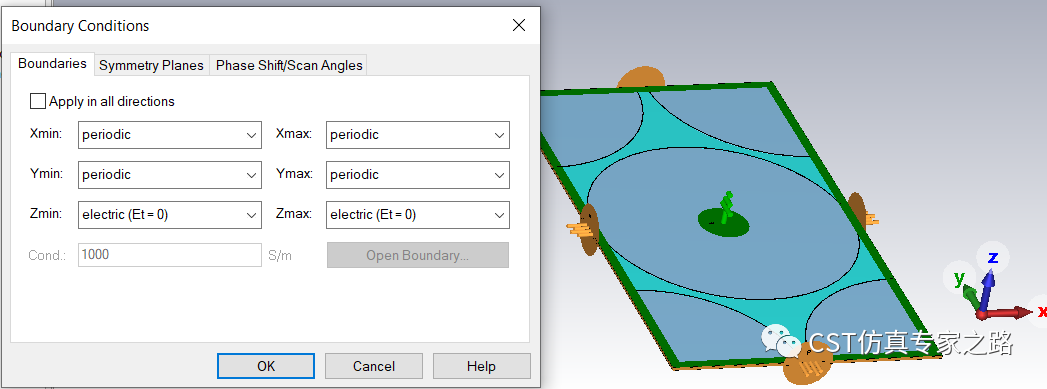
求解器設(shè)置:
提高求解器精度和速度:
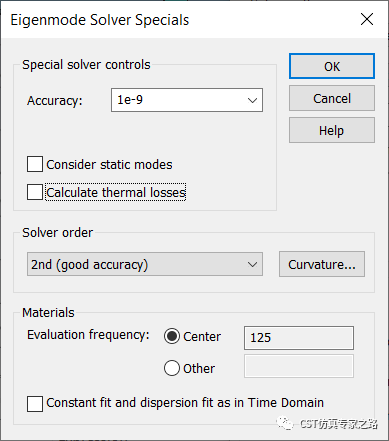
手動(dòng)加密網(wǎng)格:

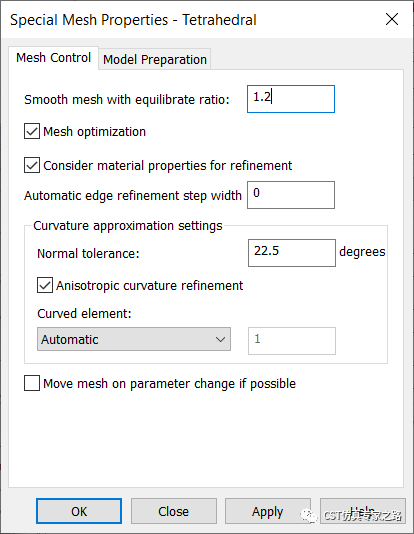
先添加后處理方便后處理:

六邊形不可約布里淵區(qū):
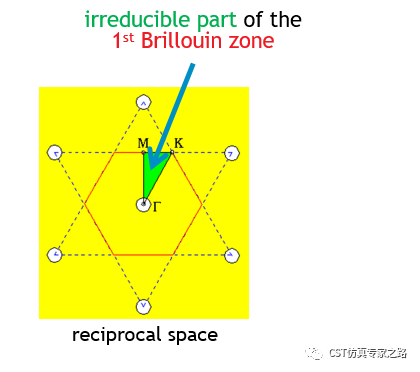
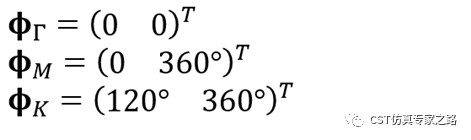
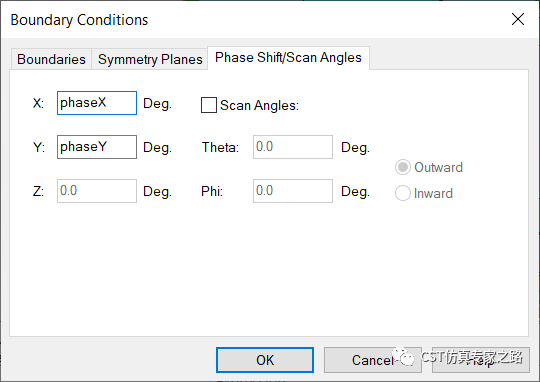
Γ→M: phaseX=0; phaseY=0~360
M→K: phaseX=0~120;phaseY=360
K→Γ: phaseX = 120~0;phaseY=360~0
所以修改phaseX和phaseY的定義式:

參數(shù)掃描開始:

第二部分:布洛赫定理驗(yàn)證


由于相位計(jì)算k的結(jié)果是非唯一解,所以該結(jié)果中會(huì)有出現(xiàn)多個(gè)Mode表示一個(gè)TM模的混亂情況。我們將通過后處理,手動(dòng)驗(yàn)證真正的TM模是哪些。
根據(jù)布洛赫定理,本征模需要滿足下式:
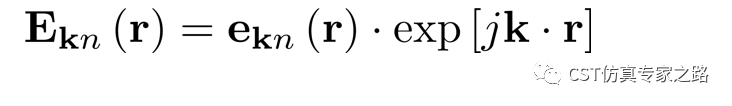
其中e是晶格周期函數(shù),E是本征模,所以,反用公式可得周期函數(shù)表達(dá)式:
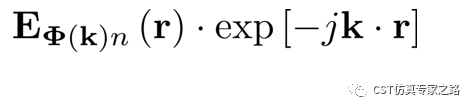
具體方法就是,在三維結(jié)構(gòu)中,我們定義兩個(gè)圓曲線,相對(duì)位置為晶格矢量,然后分別計(jì)算曲線上的Z電場(chǎng)(TM模)或Z磁場(chǎng)(TE模),然后與相位因子exp相乘,作為滿足晶格周期函數(shù)的本征模電場(chǎng),再和之前計(jì)算出的15個(gè)Mode相比較,選出符合布洛赫定理的Mode。
由于場(chǎng)數(shù)據(jù)存在采樣誤差或其他誤差,我們不能期望提取的函數(shù)表達(dá)式完全準(zhǔn)確(也沒必要),所以可用統(tǒng)計(jì)學(xué)中的變異系數(shù)(Coefficient of variation),比如設(shè)個(gè)闕值0.05,小過這個(gè)值我們就認(rèn)為兩組數(shù)據(jù)相同。相同的區(qū)域就保留Mode曲線,不相同就是不符合布洛赫定理的無效Mode曲線。
WCS放到角上,厚度中心,以該點(diǎn)為參考,定義兩個(gè)WCS的坐標(biāo),方便我們計(jì)算晶格矢量。

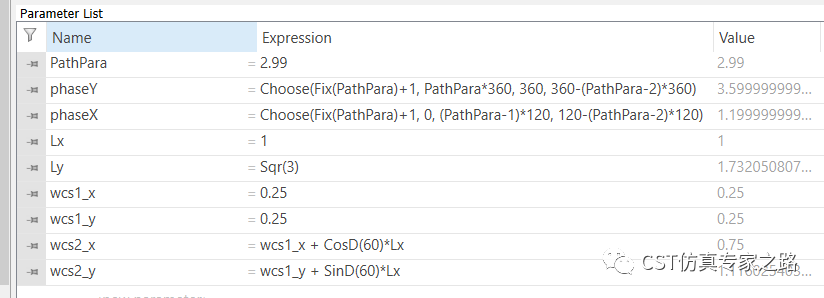
將WCS移到第一個(gè)點(diǎn),儲(chǔ)存為wcs1,畫個(gè)圓半徑0.2,所以該圓是以u(píng)軸開始的逆時(shí)針方向。


再將WCS對(duì)齊到第二個(gè)點(diǎn)(可用pick point from coordinates,需還原WCS到參考點(diǎn)), 儲(chǔ)存為wcs2,畫個(gè)圓,注意要分開成第二組曲線。


有了兩個(gè)Curve之后,后處理分別對(duì)兩個(gè)Curve提取Z方向每個(gè)模式的電場(chǎng):
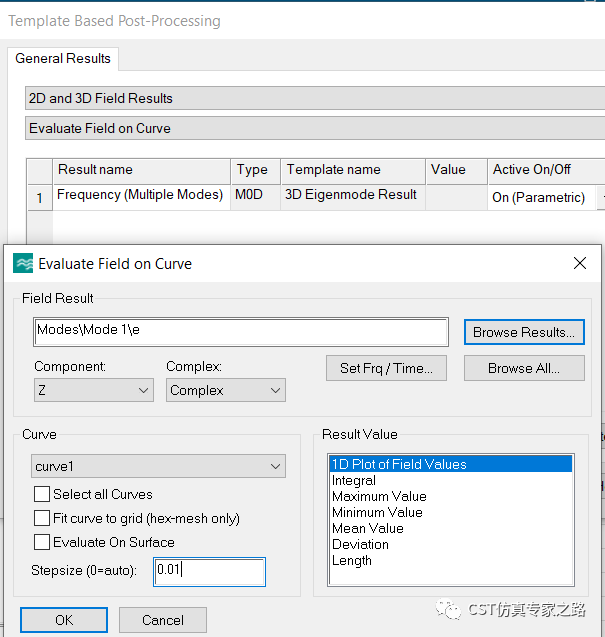
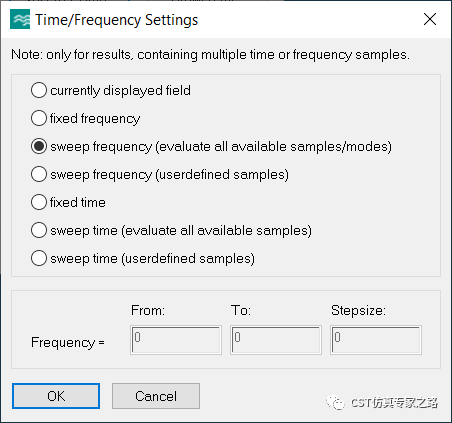

由于參數(shù)掃描并沒有記錄全部的電場(chǎng),這里可能需要重新參數(shù)掃描。結(jié)果如下:

圓曲線的長(zhǎng)度定義是從X+方向?yàn)?,逆時(shí)針轉(zhuǎn)的。不確定的話可以對(duì)比三維的場(chǎng)強(qiáng)變化來確認(rèn)長(zhǎng)度定義。
下面將電場(chǎng)與反向平面波相位因子相乘,得到curve1的周期函數(shù)表達(dá)式:
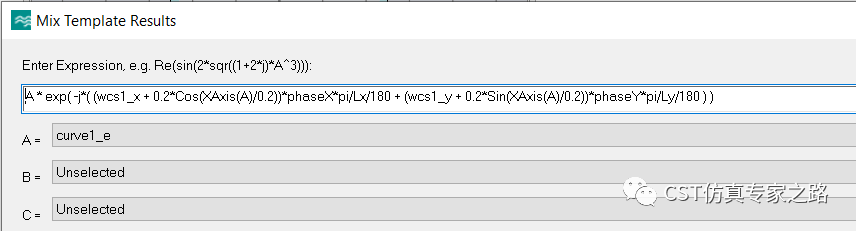
公式用到的向量關(guān)系如下:

分別計(jì)算兩個(gè)curve上的周期函數(shù)表達(dá)式:
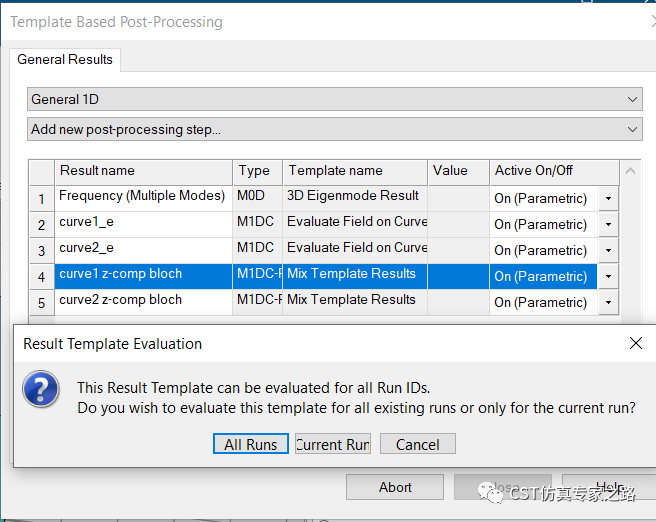
這個(gè)MixTemplate可以不用重新參數(shù)掃描,結(jié)果如下:

然后curve1的周期式減去curve2 的周期式得到誤差值:
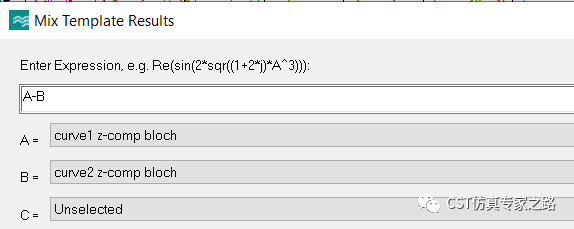
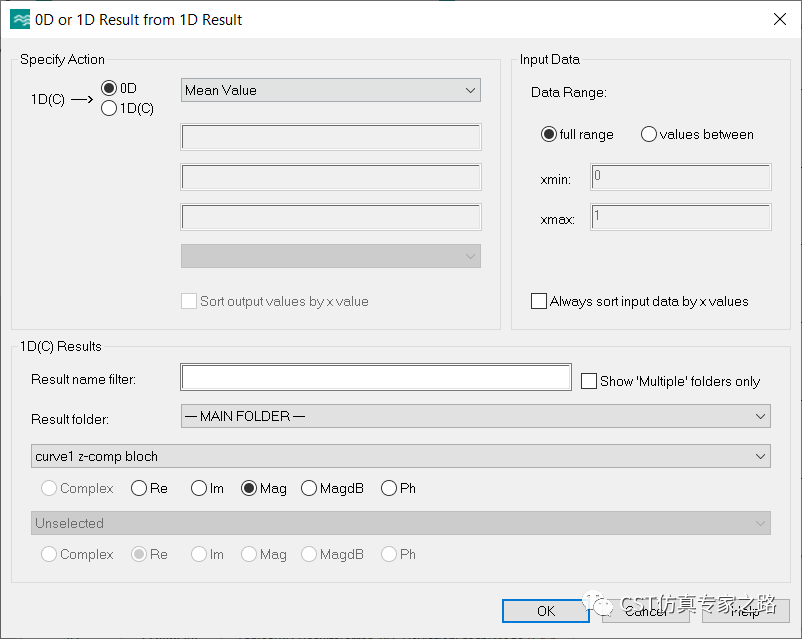
由于數(shù)據(jù)都是離散采樣點(diǎn),所以要用Stochastic的方法計(jì)算標(biāo)準(zhǔn)差:這里取實(shí)部就可以了,因?yàn)槲覀冏詈笾恍枰唤M實(shí)數(shù)來做決定,通過或不通過之前計(jì)算的這些Mode值而已。并且,這里如果選Mag, 并不能給我們有效的信息,因?yàn)橄嗤腗ag,也可以是不同的實(shí)部虛部。
所以在這一步,數(shù)據(jù)類型正式從電場(chǎng)復(fù)數(shù)變成實(shí)數(shù)(1DC變0D)。
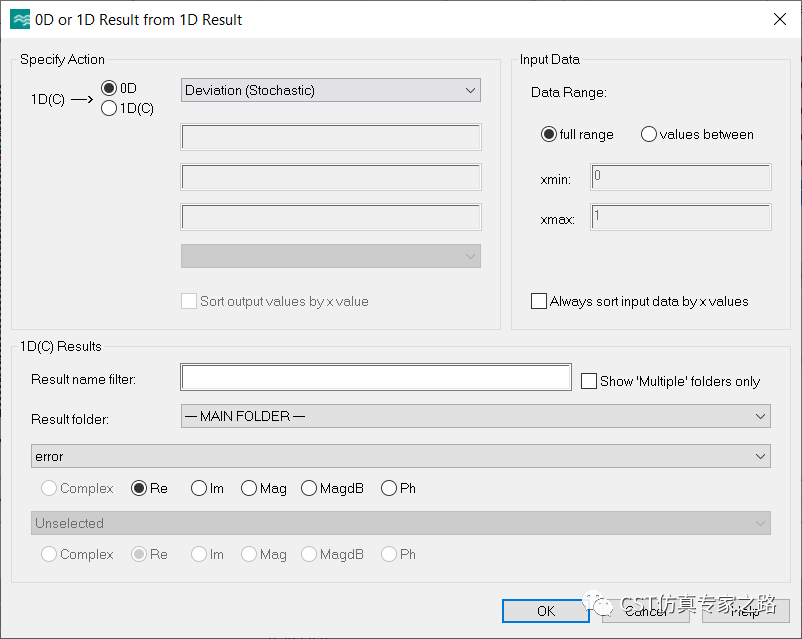
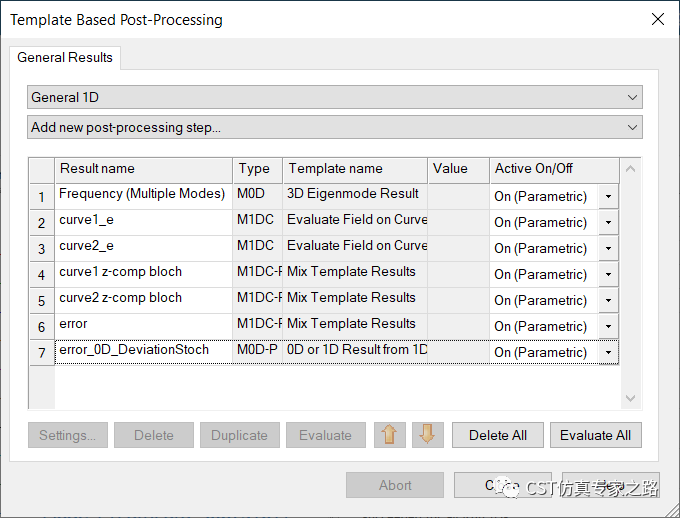
標(biāo)準(zhǔn)差值如下,其實(shí)這里就可以看出一些我們想要的結(jié)果了,就是近乎0值的這些區(qū)域說明就是滿足周期函數(shù)。

為了得到通過或不通過這樣的二進(jìn)制數(shù)據(jù),我們用標(biāo)準(zhǔn)差除以curve1的幅度平均值,得到變異系數(shù):

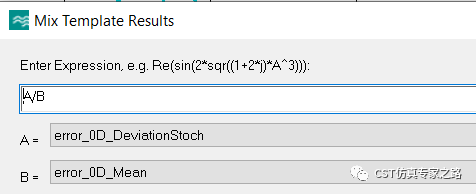
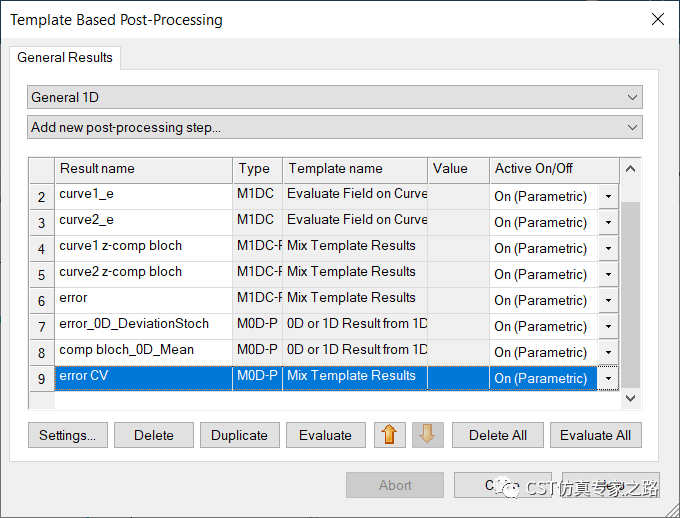
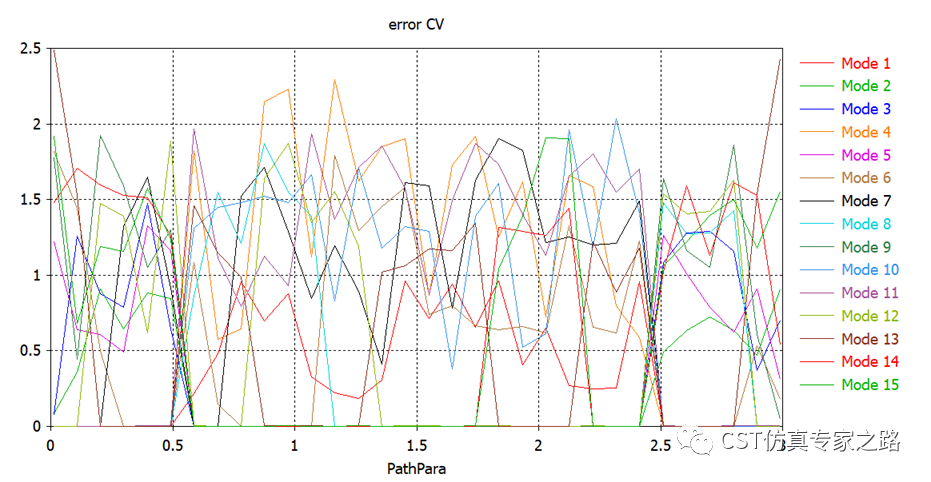
選取變異系數(shù)小于0.05的參數(shù)PathPara為1,其他為0:

將結(jié)果與之前的色散圖相乘,獲得新的色散圖:


調(diào)整曲線為相同的點(diǎn):

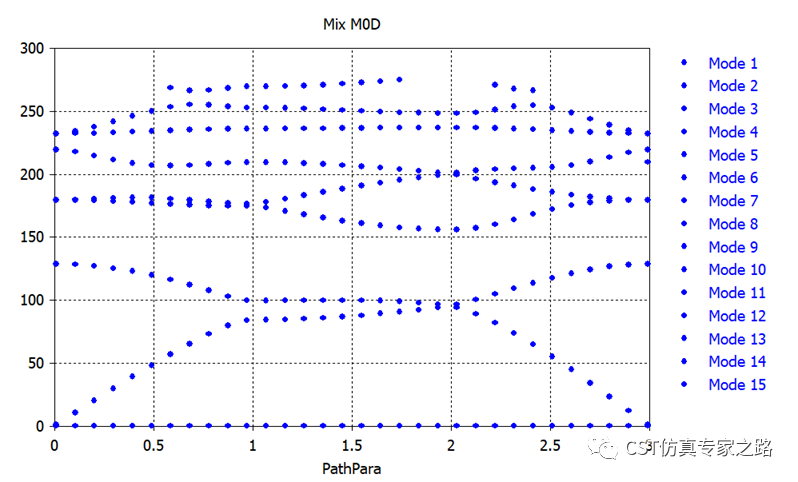
可將Y軸歸一化,晶格周期是1um:
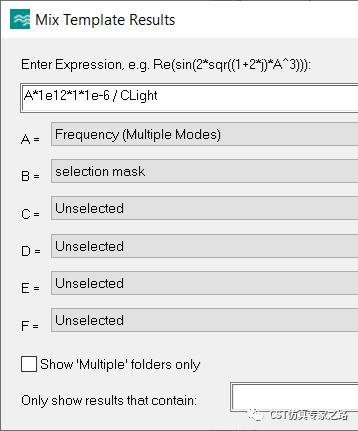
全部的后處理:
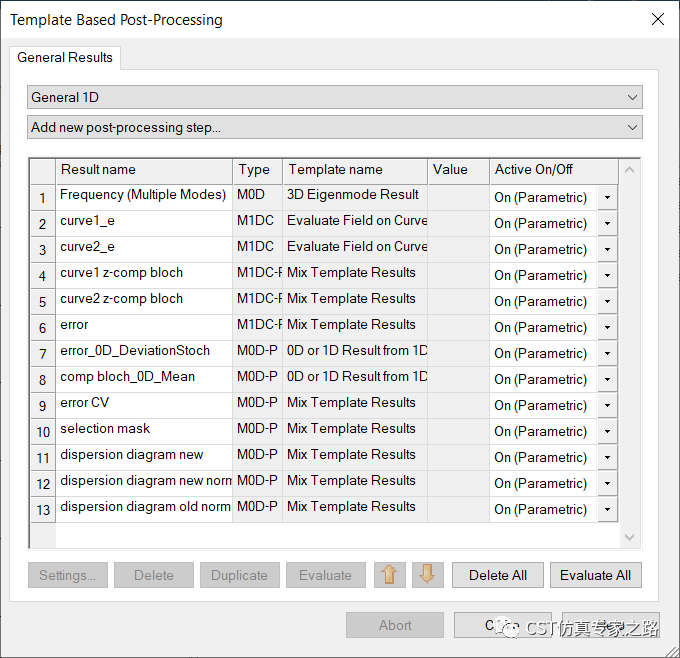
將新舊色散圖放一起,可見真正的TM模式被標(biāo)注出來:

結(jié)果與文獻(xiàn)中的TM模式一致:

參考文獻(xiàn):
J.D. Joannopoulos, “Photonic Crystals:Molding the Flow of Light”, Chap. 5
小結(jié):
1) 文中的模式式TM,如果要看TE,邊界要改成Magnetic,curve上要看Z磁場(chǎng)。完整的能級(jí)分析需要TE和TM。
2) 可能有人好奇,為什么要看圓型curve呢?其他curve行不行?我覺得理論上可以,不過圓形上的點(diǎn)坐標(biāo)容易寫,sin和cos就行,圈定的區(qū)域也比較有代表性。
3) 本文還用了一些統(tǒng)計(jì)學(xué)的手段,研究?jī)山M數(shù)據(jù)的重疊情況。
4) 60度角的晶格需要我們調(diào)整布里淵區(qū),就是CST中的ParaPath參數(shù)定義式,文中是90度的XY,以后我們會(huì)寫關(guān)于60度的XY以及更容易獲得布洛赫模的方法。
5) 手動(dòng)驗(yàn)證布洛赫定理公式成功~ 手動(dòng)雖復(fù)雜,但是可以學(xué)的更多~





