電磁熱耦合計算探討五-CST篇
今天續寫一下電磁熱耦合的計算,借著一個最近的計算項目的名義探討研究下CST中低頻工作室的電磁熱耦合仿真方案和技術要點,圖片部分打碼請諒解。
本文通過計算這個項目探討用CST計算電磁熱耦合的方法、優缺點。
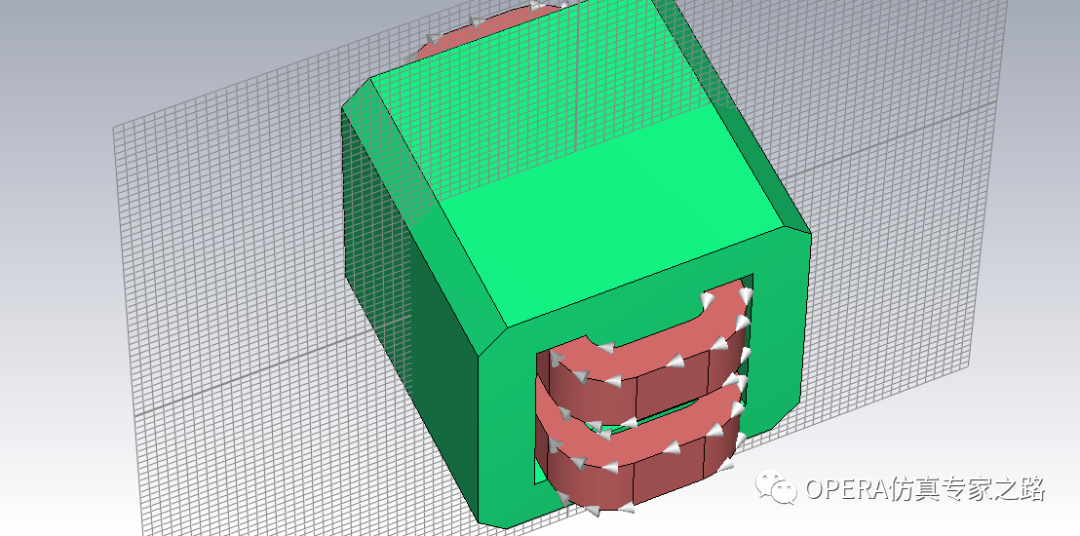
先簡單介紹下項目,模型當做變壓器處理即可,線圈電流同向,通三角波電流,鐵心用軸向無取向硅鋼片疊成,求溫度分布。
大概的圖如下:
首先回顧下好久好久之前寫的電磁熱耦合仿真探討一、電磁熱耦合計算探討二--難點、電磁熱耦合計算探討三、電磁熱耦合計算探討四--完結,難點是材料的熱導率、電導率、別熱熔、相對磁導率都是與溫度相關的。比熱容和相對磁導率在一定溫度下還會表現出和溫度非線性的關系。當電磁場和溫度場的時間步長差距太大,計算方案是電磁場計算穩態場,溫度場計算瞬態場。將電磁場的一個電周期內的發熱功率計算出來,然后插值到溫度場,計算瞬態溫度場上升直到升溫比如10度,這時候材料屬性根據溫度的上升也重新修正,然后繼續插值過去計算溫度場,可以加入停止條件為溫度場不再上升停止,也可以不加就一直計算到總時間步。大致邏輯圖如下:

如果用Opera解決這次的項目,比起《電磁熱耦合計算探討的四》的項目的區別是:這次的輸入波形是三角波,電磁部分不適用穩態求解。
Opera是個開放的平臺,辦法總比困難多,可能有這么幾種方法:
1:需要改下comi,將Opera的計算方案中的電磁導出發熱功率table的部分,變化為瞬態出場周期內多個采樣點的導出table再取個平均損耗得到的table文件。
2:將三角波激勵分解成多個穩態解累加,還是要改comi但要注意,激勵頻率不同某些材料屬性也會變化。
3:找一個總損耗近似的穩態電磁代替,畢竟是金屬傳熱,只要總損耗和分布大致保持一致,結果預期是絕對可接受的。
以上方案都可行,但是,我沒這么做。原因之一是我100%確定Opera可以考慮全部因素將上面的方案都實現的很好,原因之二是我忙(懶),畢竟公眾號文章都好久沒更了,不想去花時間驗證這么一個100%確定的事情。
那好,咱們來看看CST能不能搞定這事,優缺點是啥?畢竟CST是一個以全波方程高頻為主的軟件,他的使用習慣邏輯是否符合我們的需求呢?
讓我們用新手探索的方式展開介紹:
從第一步導入模型開始(當然先使用模板,設置個單位不能搞錯咯),我就要忍不住夸他了,哇塞,一大堆密密麻麻的格式,看著就舒服,參數化模型導入、EDA導入、STL帶網格模型導入、甚至連競品的格式都支持都有。
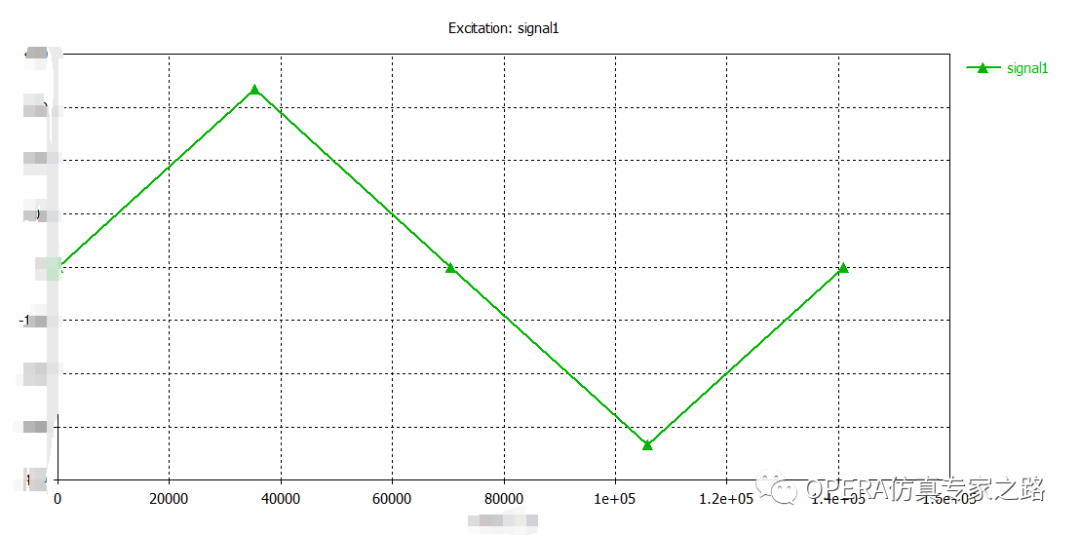
用LFT時域求解器,建好線圈加個時間VS電流激勵,(部分數值隱藏):
然后得設置下鐵心的材料,這里可能會有兩種選擇,
1.用normal的非線性材料設置BH曲線,結合疊壓系數的考慮,可以很真實的描述硅鋼片的非線性磁特性及各向異性電導率:

注意這時的BH曲線是不能設置溫度相關的,是灰色的,只有頻域求解可以使用。
但是咱知道JH和BH是可以互換的,CST會默認使用JH曲線的是硬磁材料是不考慮疊壓的(從疊壓系數是灰色就可看出來),JH可以和溫度相關,應該很多人不習慣吧。

這時的電導率,是不能設置和溫度相關的,只能設置和時間或者用J VS E的形式描述。
2.另外還有一種可能的設置,不用normal類型材料,用Temp.depende類型
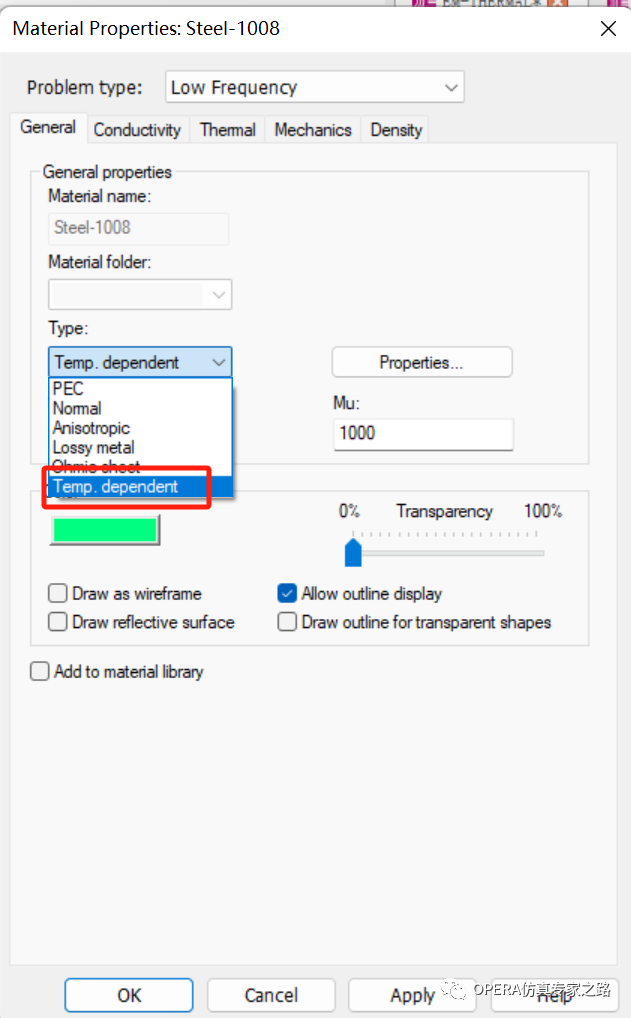
點開屬性設置會發現能設置溫度相關“線性”電導率、磁導率、介電數

熱材料屬性方面,熱導率和比熱容可以設置和溫度相關:

接下來看下CST計算電磁熱耦合內置的幾種方式:

共三種:單向電磁熱,雙向電磁-穩態熱和雙向電磁-瞬態熱。
其中:
單向電磁熱支持:【時域、頻域、全波頻域、直流電】+【穩態熱、瞬態熱、共軛熱】
雙向電磁-穩態熱支持:【頻域、直流電】+【穩態熱、共軛熱】
雙向電磁-瞬態熱支持:【頻域、直流電】+【瞬態熱】
結合項目,我們可以預估其溫度變化不會特別夸張,但是因為用的交變電,故BH曲線的磁密相應導致的渦流變化還是很重要,所以放棄用線性溫度相關的Temp.dependent類型材料定義。缺陷是不考慮電導率的溫度變化,但這個可以根據最終溫度去手工迭代下。其他的熱材料屬性都設置和溫度相關。
咱先采用時域計算方案,所以用單向電磁熱即可。既然溫度不反向影響電磁材料了,那正好BH不能設置溫度相關也就無所謂了,本來這點溫度對BH曲線的影響也不是特別大。鐵心發熱由于鐵損引起的,CST內置的流程邏輯是導出一個電周期內的平均渦流損耗給到熱計算,也可以計算出總鐵損,但是不可以給到熱求解。這時就需要判斷下的磁滯損耗比起渦流損耗是否可以忽略,如果不能忽略也只能用在導入的時候用scale去根據磁滯損耗和渦流損耗的估算比例去修正下。
電磁部分大致這樣了,熱學里面的難點就是設置下鐵心表面的熱交換系數,有些經驗公式或者參數參考,一般5到25范圍,我第一次折中了下選的10。然后咱看下穩態熱的結果,差不多260度左右:
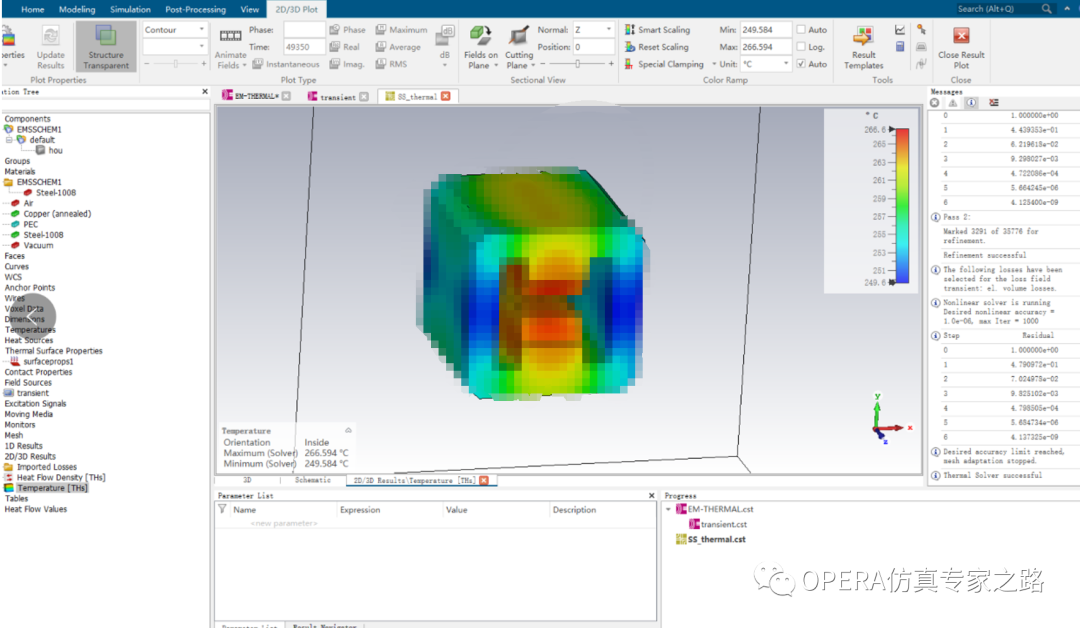
再看看用瞬態熱耦合結果,也是260度左右(截圖250是我沒標尺沒截好,因為后面改了參數了所以沒法再截圖了):
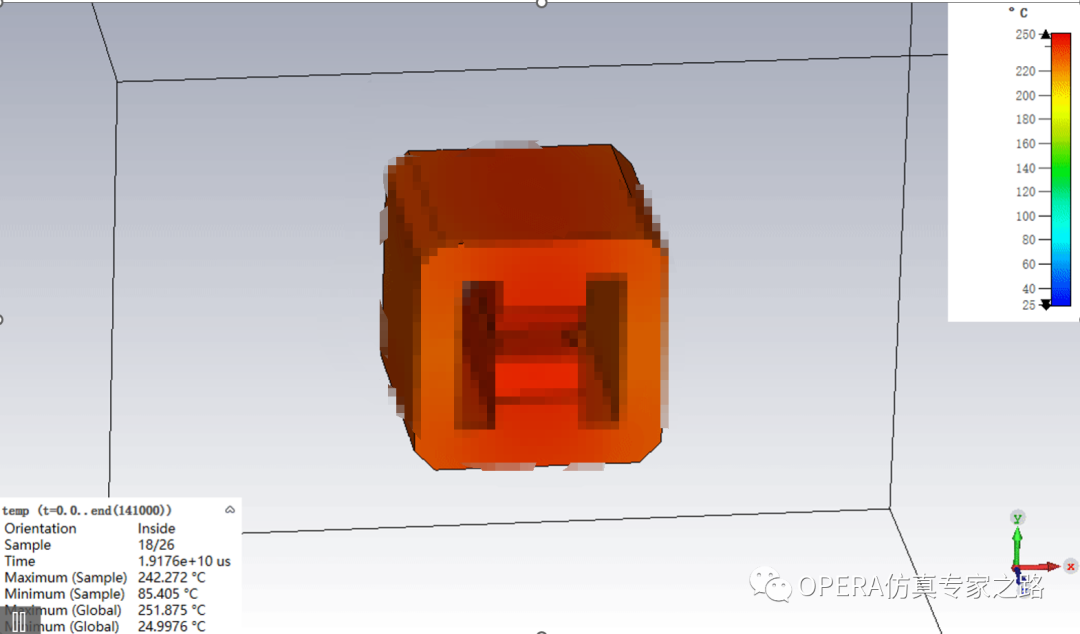
然后咱切換到共軛熱求解器去耦合,這時候考慮了氣體以及使用了湍流模型了,就不需要表面換熱系數了。
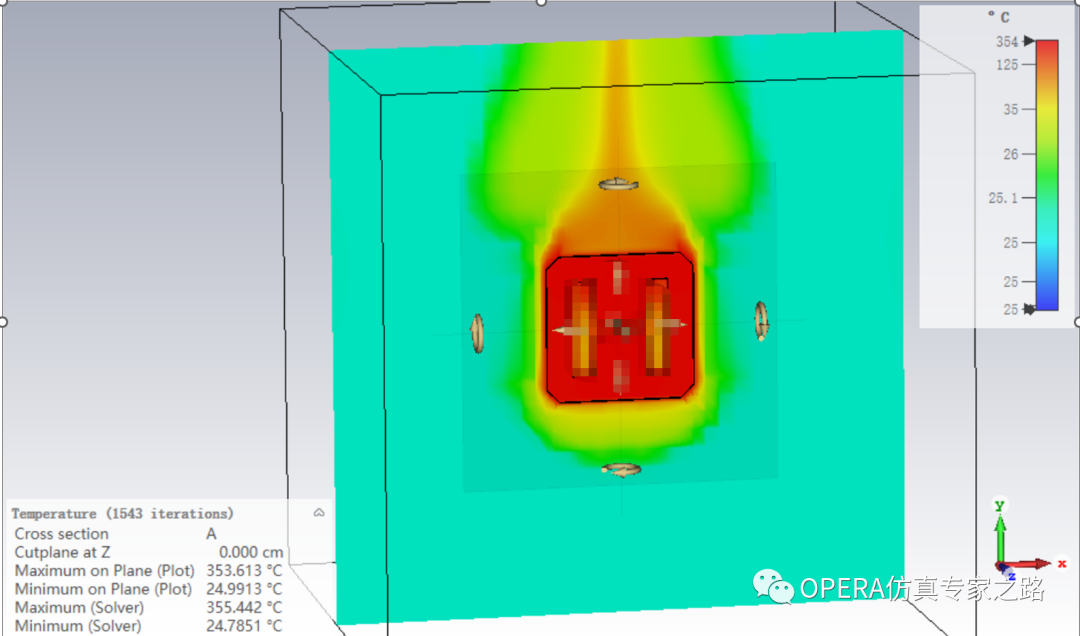
這結果看著是不是更酷,可惜這時候發現溫度計算出來居然有350度左右,多了足足100度,看下表面散熱系數,發現都在5左右:

問題找到了,將之前穩態熱和瞬態熱的表面換熱系數從10修正到5再看結果,穩態熱:
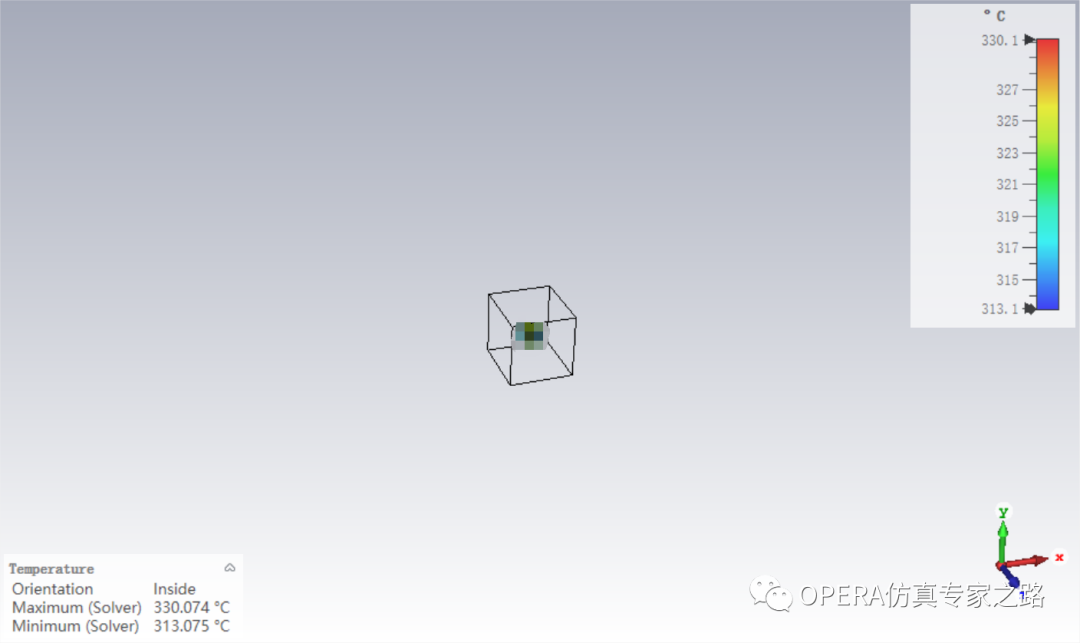
瞬態熱:

都在335度左右。三種熱求解器可以比較完美的對上咯。共軛熱中的表面換熱系數處處不同,造成了瞬態和穩態熱的結果稍有區別。
可見單向電磁-熱耦合最佳方案就是,時域電磁+共軛熱的方法。此仿真方案與實際情況比忽略了一部分磁滯損耗(通過損耗比例可調節),電導率沒有考慮溫度變化(通過最終溫度迭代電導率),BH曲線沒考慮溫度影響(無能為力)。目前看該方法和實驗校對是比較好的。
至此單向電磁熱耦合計算完了,然后可以嘗試把電磁部分改用等效頻域計算,使用雙向頻域電磁-穩態熱,那么就可以使用BH曲線溫度相關了,也會是很好的一種方案,今天先戛然而止了。
對比OPERA完全開放想咋弄就咋弄但需要人做很多事,CST雖不能面面俱到,但是非常便捷高效,在用戶結合自己項目的實際情況選擇較好的方案時可以高效的得到非常好的結果。





