CST MWS同軸連接器自適應網格優化發現的一個有意思的地方
閑暇之余,按照《微波工作室用戶全書》卷二的同軸連接器的例子做仿真,結果發現了一個非常有意思的地方,采用自適應網格加密(Energy based&Expert based)后,查看結果的Mesh Adaptation Logfile,結果發現Pass2計算速度居然比Pass1快,很是驚訝!因為自適應加密后,Pass2的網格數是Pass1的23倍,理論上應該Pass2的仿真時間更長啊。
Energy based: Mesh Adaptation Logfile
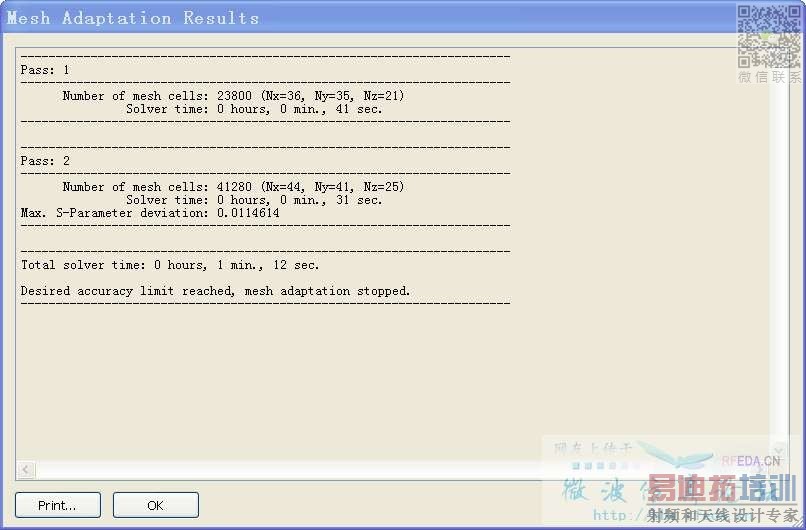
Expert based: Mesh Adaptation Logfile
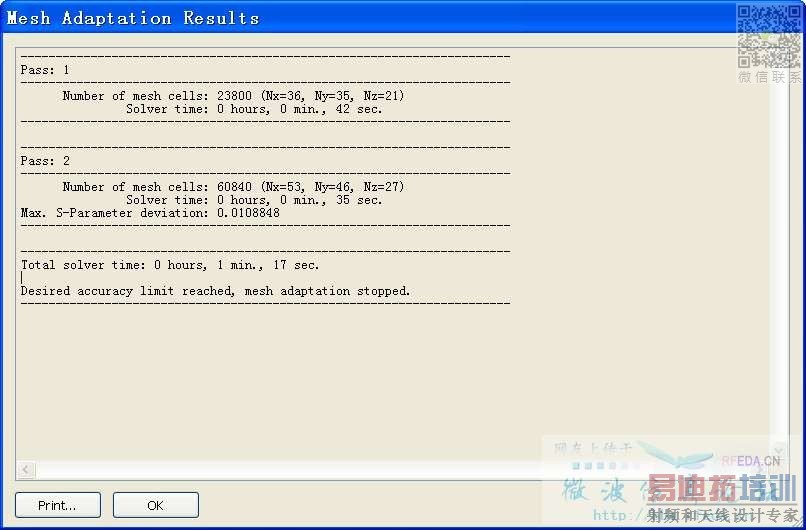
不知道大家有沒有研究過這方面的情況?
我猜的是,加密后的情況只計算了加密的部分,未加密的地方沒有進行計算。
我覺得在第二次加密的過程中可能出現網絡的最小分辨率變大,網格總數比第一次的網格總數多。而且計算總的時間與網格數目以及網格的分辨率是有關系的。所以出現上述的情況應該是合理的。
而且除此之外,第二次計算時可能不需要重復第一次的某些初始化計算,因此可以減少這部分的時間。
在優化中,也會出現第二次優化的時間比第一次短的情形,雖然網格總數目沒有變化。
你說的最小分辨率變大的情況不成立,因為Adaptive mesh refinement是朝著加密方向優化的,因而網格密度只會增加或者不變,絕不會減小,下圖為證
Energy based Global Mesh
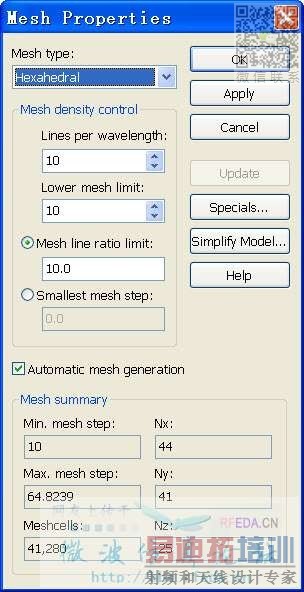
Expert based Global Mesh
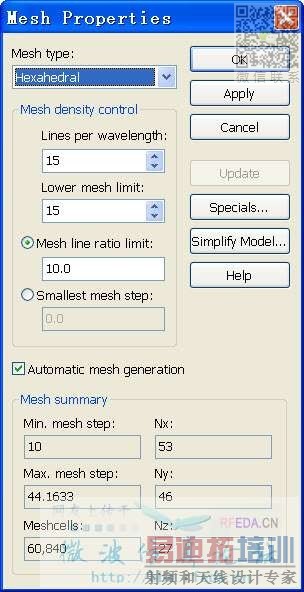
No refinement Global Mesh
初始化計算這個概念太籠統了,缺乏根據和說服力
要是這樣就好了,如果網格數表較多的情況下進行優化,也不會占用太多時間;不過CST有這么智能嗎?可以分著算嗎?希望有算法方面的高手給詳解
以下是個人理解,僅供參考。
首先,1樓的情況可能只能通過CST官方解答了。只看幫助文件《The Simulation Method》好像并沒有明確指出電磁場參數只在單個網格內計算還是會受到相鄰網格計算數值的影響,不了解具體的算法原理,不能確定。因此不知道如果網格大小保持不變的話,Solver是否會保存上一次的計算結果。
第二,每次adaptive mesh,都要重新進行初始化計算,所以2樓所說的后半部分是不正確的。當然,2樓的前半部分也持保留意見,這個應該不可能出現。
第三,小編的這個模型solver的計算時間很短,很難判斷是哪個“環節”的時間被縮短了,excitation duration、matrix calculation time、solver setup time、solver loop time、solver postprocessing time,這些參數哪些變化了哪些沒有變小編給出的數據體現不出來。
第四,并不能說網格數增加仿真時間就必定延長。有沒有可能在“大網格”條件下模型內的能量因為“諧振”而耗散得慢,在“小網格”條件下計算沒有出現“諧振”因而能量耗散得快?我想沒有人可以很確定得回答是或者不是吧。
建議:重新運行,在transient solver parameter對話框里勾選"Store result data in cache",看看能不能把每一次的solver logfile保存下來。如果不能的話,有可能需要通過VBA把solver logfile保存起來,先要確定是哪個環節的時間被縮短了。
收兵回營!
有一點我沒搞明白,為什么大網格下諧振 小網格下不是諧振。 一個微波元器件是否諧振應該是其自身的屬性 應該不是由網格決定的吧
網格數決定了模型離散化導致的誤差大小,按照你的說法,應該是大網格下的誤差太大了。你通過自適應網格優化看delta S變化就可以看出誤差的大小
的確不是由網格決定的。
但是對于這個問題的理解是這樣的,不是說網格決定了結果,而是結果就在那里,你用更加準確的網格可以得到正確的諧振,而不夠密的網格可能對模型剖分不夠精確,得不到該得的結果。
正所謂,你加密或者不加密,微波元器件諧振就在那里,不偏不倚。
這兩天事情多把這個帖子忘了……。
上面兩樓的分析都是有道理的,用誤差或者準確性來解釋個人認為都是合理的。當然,在網格變化的時候有可能會造成諧振頻率點變化。假設一個極端的例子,網格變化導致諧振頻率點移出了仿真頻率范圍,仿真速度會不會加快呢?以上純粹猜想,僅供參考。
1.仿真時間好像跟諧振頻率沒什么關系,因而仿真時間不會因為諧振頻率的變化而變化;不過,網格都變了(你說的諧振頻率變化由網格變化引起)仿真時間一定也會變化
2.存在強諧振的結構是不是S參數隨網格數變化很大啊?最近仿真了一個強諧振天線Energy based網格優化Pass8都沒滿足delta S<0.02要求。不過諧振頻率從Pass開始就很穩定變化不大感覺你的猜想非常極端
我說的是一種假設情況,并不是針對你的模型。仿真時間確實跟諧振頻率沒有關系。
自適應優化每次之間的變化大小只跟模型自身結構有關。假設模型的“關鍵區域”結構不復雜,那么Pass之間不太可能出現明顯的變化。假如“關鍵區域”是非常精密的結構,很可能就有比較“明顯”的差距。
各位都是高手。新手順便請教個常識:所謂仿真時間,從能量的角度來看,是不是可以理解成系統饋送能量后,會計算結構中能量的殘余量的多少來決定仿真是否結束。從而引出所謂強諧振的情況能量一直在器件內震蕩導致仿真時間相對較長。這個諧振和我們說的RL上的諧振,是一回事么?
個人認為你對于仿真時間的理解是正確的。至于和RL諧振的關系,個人認為在某些情況下是有聯系的,但不認為在所有情況下都有聯系。
還有可能是....我覺得很有可能的是....
第一次仿真的時候干其他事了,比如上網,音樂,電影。CPU占用多。
第二次仿真的時候睡覺去了,CPU都給CST用了。
我就經常這樣。哈哈





