CST不同激勵信號下的S參數
相同的模型,相同的設置,只有端口給的激勵信號不一樣,得到的S參數如下:
(1)默認激勵信號
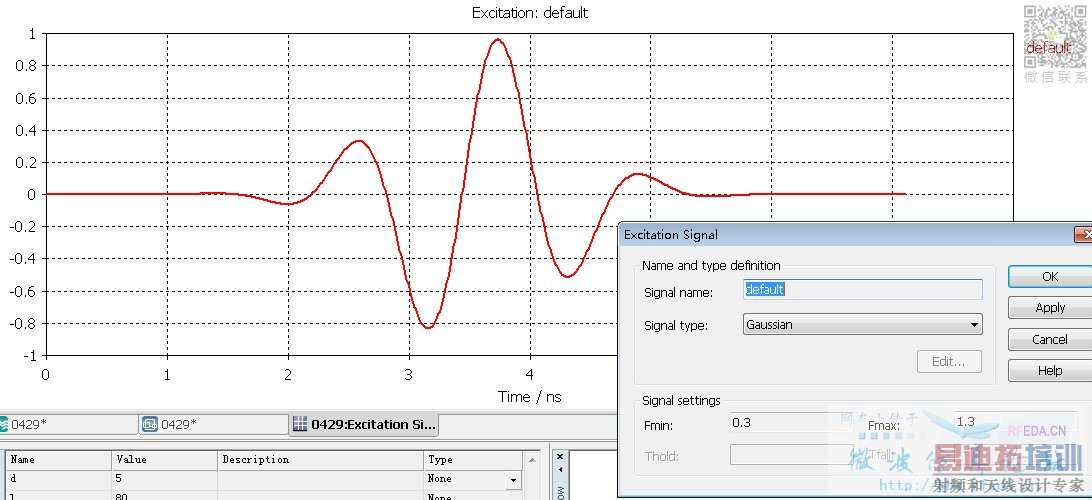
得到的S參數是這樣的

(2)正弦激勵信號
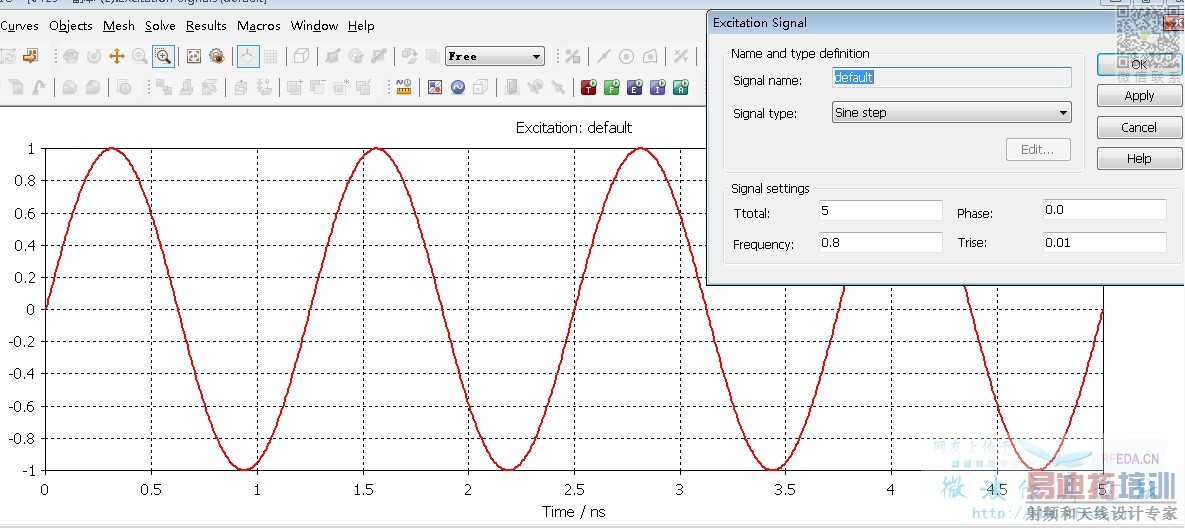
得到的S參數是這樣的

請教各位大俠(1)正弦信號里面的頻率設置只是改變它的周期么?還是說仿真結果只有這個頻點是靠譜的?
(2)不明白不同種類的激勵信號S參數為什么差這么多,方向圖差別也蠻大。我該以哪個為準呢
S參數指的是在諧波輸入狀態中得到的輸入輸出的關系。
如果分母的數字=0 你說計算的結果會靠譜嗎
你只要不用正弦信號,其他的應該都靠譜都是一樣的。
1、算頻響要采用寬頻的時域信號激勵,顯然正弦這種窄帶信號不行
2、如果不采用CST默認的時域激勵信號(gauss),如果看頻響應,應設置歸一化(下圖)
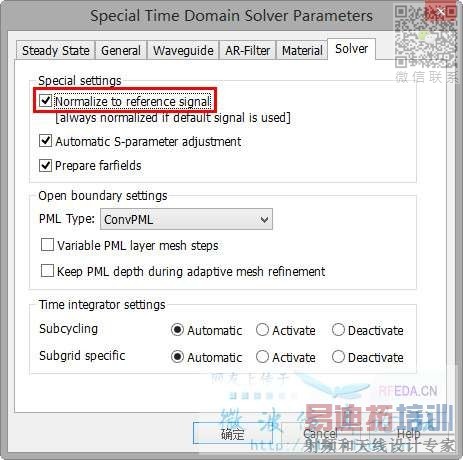
第一點好理解,
第二點中的歸一化是相對于什么進行歸一化?是對自己設定激勵信號的最大賦值為1進行歸一?其必要性是什么?不歸一難道還影響S參數?這說不過去啊。
這里只需要一點基本物理常識就可以理解了。
當你要讓CST算某一結構的在一定頻率范圍的響應情況,你有兩種選擇:
1. 采用頻域算法(頻域求解器)。對你關心的范圍進行頻率掃描,后處理一下就可以得到S參數與頻率的關系。
2. 采用時域算法(時域求解器)。此時你雖然不需要對頻率進行掃描,但這種方法對你的激勵信號提出特殊的要求,算法本身我也不了解,但就我對物理本身的理解,不同信號在你關心的頻率范圍內的能量分布是不一樣的,如果你采用頻譜非常窄的信號(比如你后面那個信號),那么時域算法在很大的頻率范圍內都算不準(因為這些頻率范圍幾乎沒有能量)。所以你采用這種時域算法,至少保證你所選取信號的頻譜覆蓋所關心的頻率范圍。一般你設置好頻率范圍以后,CST自動生成一個高斯脈沖,基本可以滿足前面的要求。
我覺得當運算量比較大時,時域算法相對于頻域算法的優勢就體現出來了。
6樓是別人回復5樓直接拷進來的?
寫得很不嚴謹。
CST MWS幫助文件《Signals in Time Domain Simulations》。
請教,哪里理解有問題?
好吧,謝謝各位了,我大概懂了
看樓上的幾位都沒說出來,在CST時域仿真中,S參數是通過對時域信號進行傅里葉變換,然后相除得到的,也就是說,以S1,1為例:
S1,1=FT(o1,1)/FT(i1)
其中o1,1是端口1的反射信號,i1是端口1的輸入信號(也就是激勵信號),FT()表示傅里葉變換
從上面的公式就可以看出,如果i1是正弦信號,那么激勵信號的頻譜除了正弦頻點不為0之外,其他各個頻點的頻譜都是0(真實仿真中由于信號長度不是無限長,所以信號頻譜并不是只有一點非0,而是存在一定的帶寬),導致了你用正弦激勵時S參數錯誤的情況。
上面的公式大家完全可以使用CST自帶的后處理進行驗證
上面的公式也說明了為什么CST選擇高斯脈沖作為激勵,因為高斯脈沖在整個頻段內,頻譜無0點
謝謝!(說的有點遲了)





