CST PIC求解器腔體微波粒子束耦合
今天一起看一個(gè)PIC求解器案例:

這個(gè)呢就是我們今天要整的一個(gè)腔體模型。
然后對發(fā)射源進(jìn)行設(shè)置,選定發(fā)射源邊界:

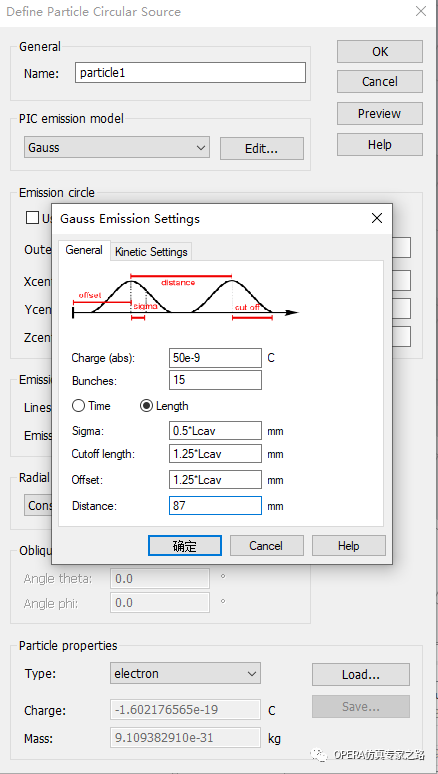
這里對Gaussian高斯發(fā)射參數(shù)設(shè)置給個(gè)基本說明:
高斯發(fā)射每個(gè)脈沖的發(fā)射電荷是一個(gè)時(shí)間相關(guān)的高斯函數(shù)。菜單里輸入指定高斯脈沖的各種參數(shù),如每個(gè)脈沖的總電荷、脈沖寬度或兩個(gè)連續(xù)脈沖之間的時(shí)間間隔。在沒有場的情況下,當(dāng)粒子具有相同的初始速度時(shí),空間上也滿足高斯分布。通過勾選“時(shí)間”和“長度”,可以分別在時(shí)間和空間維度上定義上述高斯脈沖的參數(shù)。
若使用Length空間高斯分布的情況下,發(fā)射在時(shí)間上仍然是高斯分布的,在kinetic setting動力學(xué)設(shè)置里會間接或者直接的定義初速度,空間位置參數(shù)被轉(zhuǎn)換成等效時(shí)間。
在粒子加速器中,一般高斯脈沖參數(shù)在空間已知,在空間上即Length定義高斯脈沖的更方便。
具象點(diǎn),發(fā)射源形式長這樣:

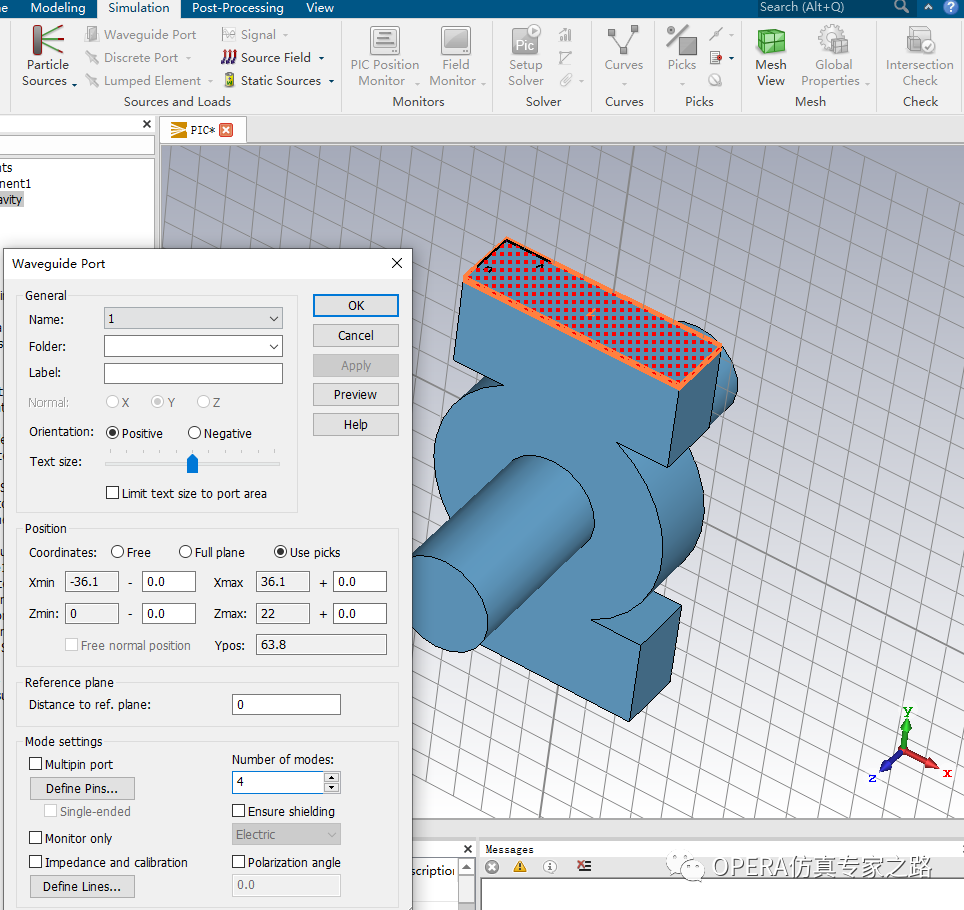
接下來定義微波輸入端口:
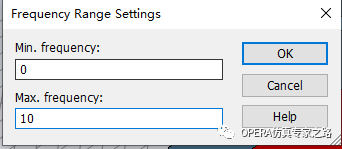
定義求解頻率:
PIC求解器設(shè)置:
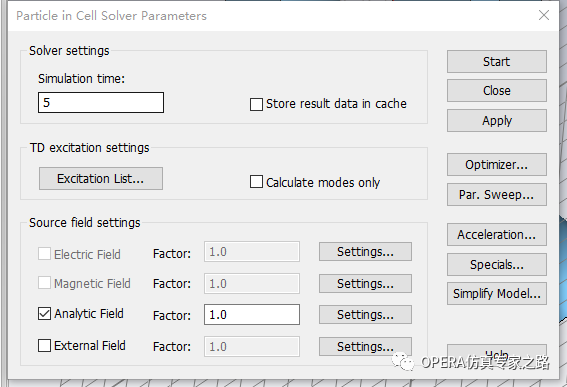
定義相空間、位置監(jiān)視器:
網(wǎng)格使用默認(rèn)設(shè)置就行,然后開始計(jì)算,計(jì)算完成后查看后處理。
軌跡預(yù)覽:
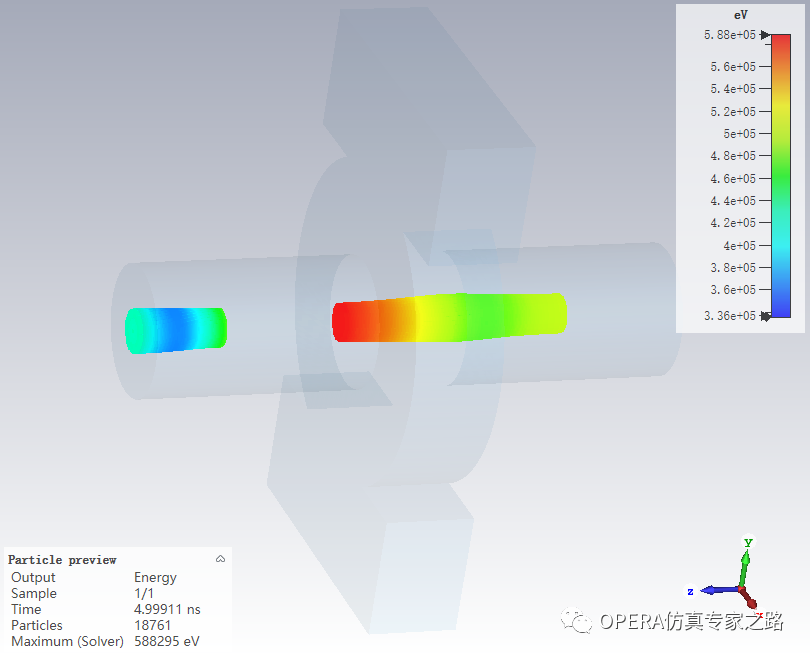
既然是時(shí)域,看一下動圖,很明顯可以看到,發(fā)射后的束流經(jīng)過腔體耦合后形狀能量都發(fā)生了變化:

然后是洛倫茲因子Gamma的相位圖:


端口1的信號顯示粒子束產(chǎn)生了高功率的無線電波:
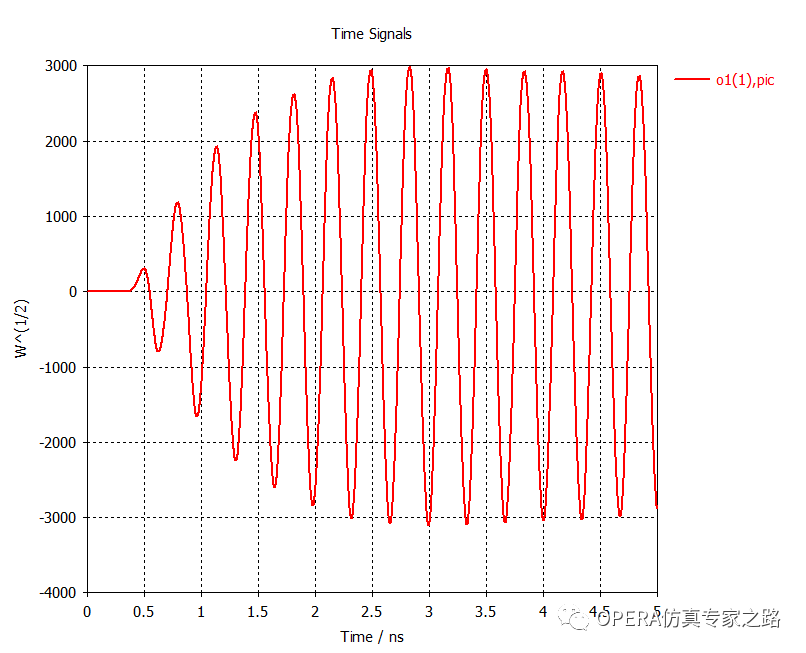
輸出信號對應(yīng)于峰值功率的平方根,計(jì)算出輸出端從波束提取的平均功率為0.5*3000^2= 4.5 MW。
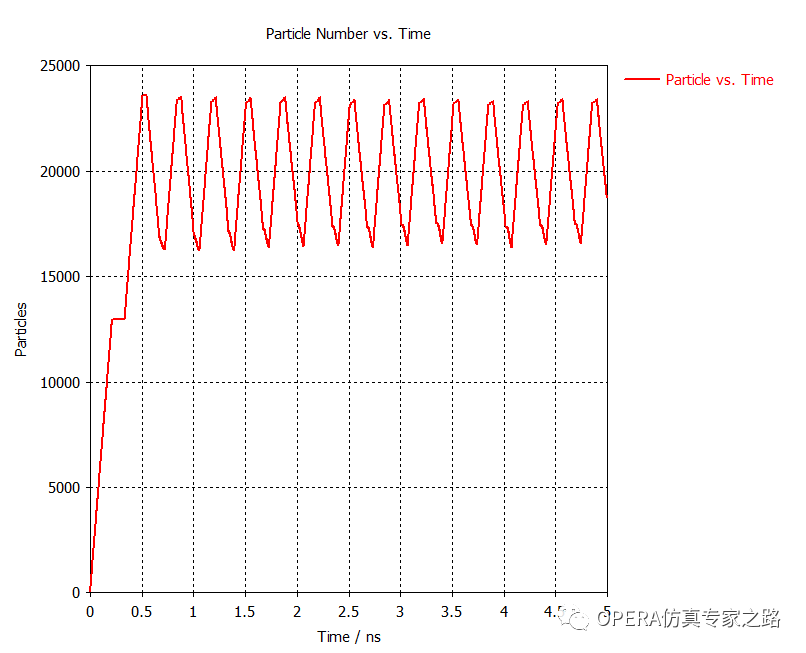
再看下宏粒子總數(shù)與時(shí)間的圖。當(dāng)源發(fā)出新的粒子時(shí),曲線增大。當(dāng)粒子撞到東西或被背景吸收時(shí),數(shù)量會降低。可以觀測二次粒子倍增的情況:
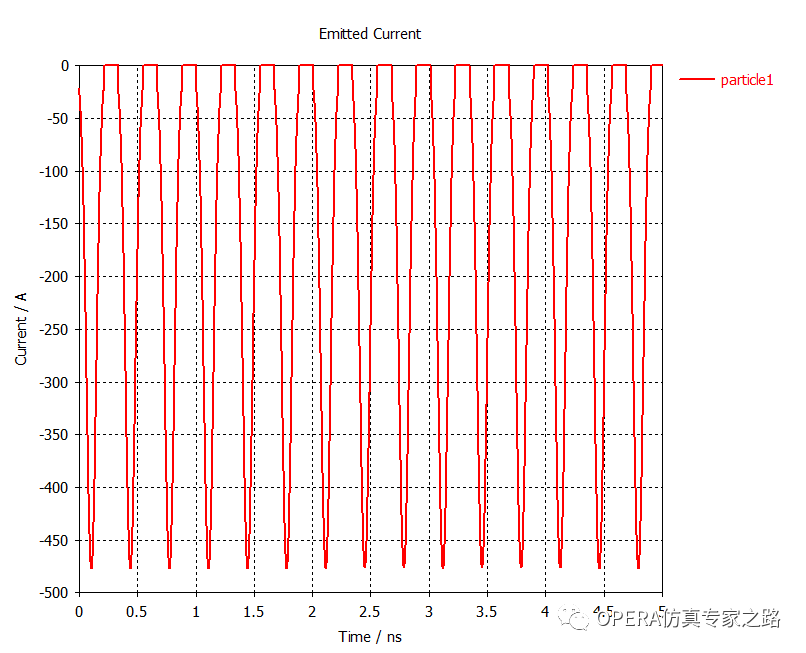
發(fā)射電流VS時(shí)間圖:
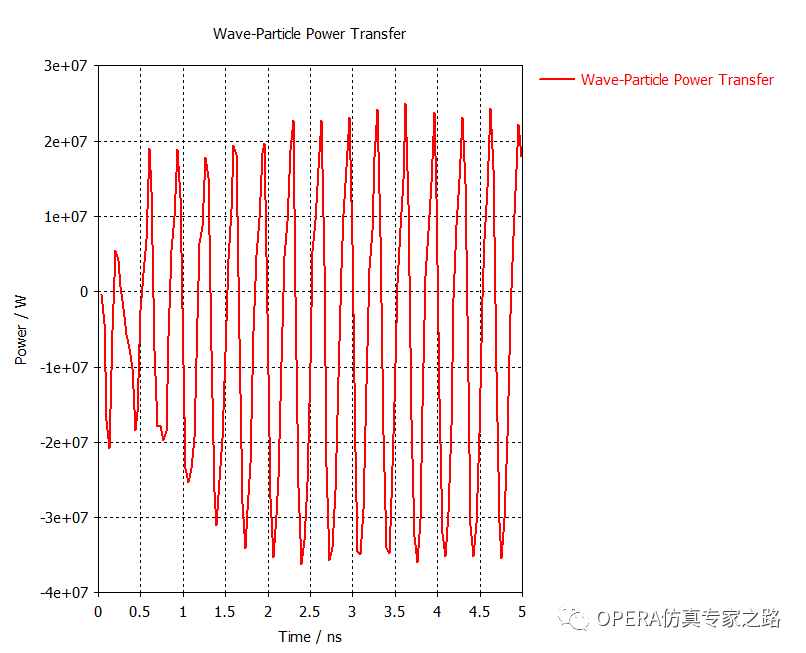
最后來一個(gè)電磁波-功率傳輸圖:電磁場從粒子上得到或者損失的功率對應(yīng)關(guān)系。
這就是今天看的案例流水賬及一般需要的后處理。





